物流产业发展与区域经济关联分析

      0 引言

      物流业是融合运输业、仓储业、货代业和信息业等的复合型服务产业，是国民经济的重要组成部分[1]。实证分析表明，作为国民经济发展的重要产业和新的经济增长点，物流业在促进产业结构调整、转变经济发展方式和增强国家经济竞争力等方面发挥着重要作用。研究区域物流与区域经济之间的内在作用机理及其协同发展模式，有助于帮助政府主管部门定位区域物流功能，促进物流产业的健康发展。

      天津和上海分属于华北物流区和长三角物流区，且均为区域经济中心城市。2009年，国务院公布的《物流业调整和振兴规划》将这两个城市定位于全国性物流节点城市。2010年，津沪两市地区国内生产总值分别为9 224.46亿元和17 165.98亿元，在全国市级排名中分别位列第六和第一。研究这两个城市物流业与经济发展的关系，能够更好地了解环渤海经济区和长三角经济区物流产业的发展现状、相互关系和未来趋势，为加快沿海地区物流产业的融合发展，促进区域物流一体化建设提供参考。

      1 文献回顾

      在国际上，对物流业与区域经济增长关系的早期研究是从航空运输与区域经济发展关系的分析中开始的。Debbage[2]在研究美国卡罗来纳州航空运输业的经济结构时发现，当地经济的变化和城市经济之间的相互联系能够影响航空运输业的发展，两者之间存在因果关系。Button和Taylor[3]的研究发现，经济增长能够刺激国际航空运输业的发展，并以此建立了一个美国区域经济增长与区域航空运输发展的关系模型。 Lee和Yang[4]通过研究航空运输与东亚区域经济发展的关系，制定了韩国仁川国际机场发展战略。

      近年来，关于区域物流与经济互动发展的研究也引起了国内学者的关注。闫秀霞和孙林岩[5]运用总量生产函数构造了物流与区域经济关系的计量模型，并分析了我国东、中、西部地区物流与经济发展的差异性。刘南和李燕[6]运用格兰杰因果检验法，从供给推动和需求拉动两个角度分析了浙江省物流业发展与经济增长之间的关系。胡凯、甘筱青和高阔[7]着重分析了中部地区物流基础设施投资与经济增长的关系，发现物流固定资产投资对经济发展具有单向促进作用。此外，张炜熙、胡玉莹和温泉[8-9]对物流业与经济发展的互动关系也进行了有益的探讨。

      从目前的研究看，对于物流业与经济增长关系的研究主要集中在单个经济区域，尚未有学者涉及对多区域物流与经济关系的比较分析，同时对两者的动态作用机理也缺乏定量分析。为此，本文进行了两点创新：①在问题设计上，以天津、上海两市为实证研究对象，比较两个不同地区物流业与经济发展关系的异同点，为促进区域间的物流融合和协同发展提供必要的政策建议；②在方法运用上，通过建立向量自回归模型(VAR)，运用各变量产生的脉冲响应函数对物流与经济发展协调关系的动态传导机制进行定量分析。

      2 津沪物流与经济增长关系的实证分析

      2.1 指标与数据选取

      本文从物流成效(CX)、物流供给(GJ)、物流业投资(TZ)和物流需求(XQ)4个层面考察津沪两市的物流业发展情况[6]。在物流成效层面，主要选取交通、仓储及通信业产值指标表示物流产值，衡量物流发展的程度；在物流供给层面，主要选取物流网络里程指标反映津沪两市的物流供给状况；在物流业投资层面，主要选取交通、仓储及通信业的固定投资作为物流业投资指标。此外，选取货运周转量作为反映物流需求的指标；在经济发展方面，主要选取地区国内生产总值(GDP)作为衡量经济发展速度的指标。

      本文选取的数据样本区间为1995—2010年津沪两市的官方统计数据[10-11]。为消除物价变动因素产生的影响，物流产值、物流业投资和地区国内生产总值对1978年的不变价格作平准处理。同时，为消除时间序列数据存在的异方差，本文用各时间序列数据的自然对数进行平稳性检验和关系分析，这种处理并不影响变量之间的协整关系[12]。取自然对数后各变量的标识为LNCX、LNGJ、LNTZ、LNXQ和LNGDP。图1显示了天津和上海物流发展与经济增长的趋势关系，从中我们可以看到，各变量均具有上升趋势，且上海市物流业的发展与经济增长更具相关性。

      

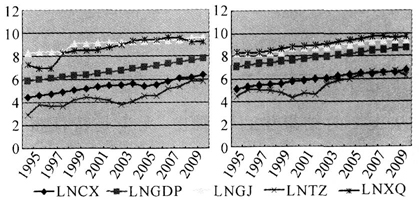
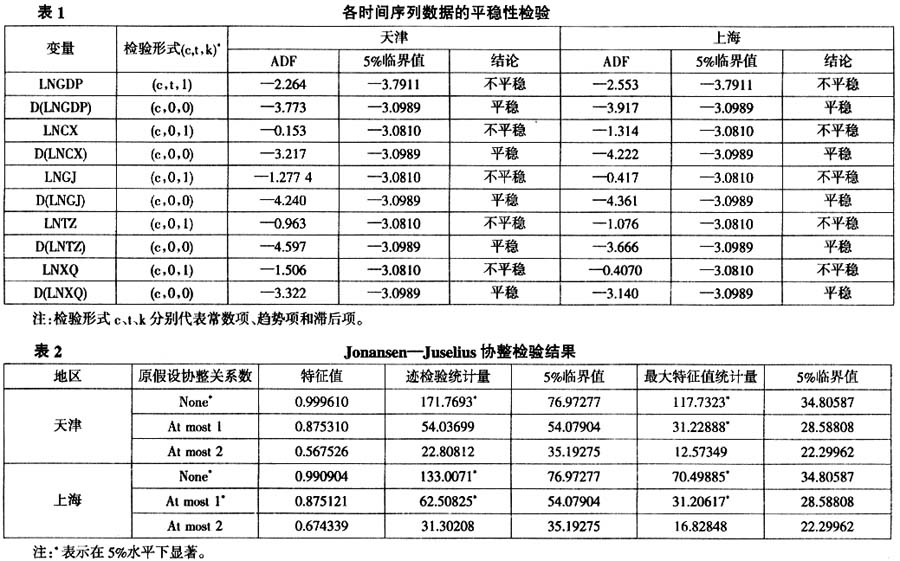
      图1 津(左)、沪(右)物流发展和经济增长的趋势关系

      2.2 津沪物流与经济增长的因果关系检验

      本文首先选用格兰杰检验方法对津沪两市物流与经济增长的关系进行因果关系分析。格兰杰检验是由诺贝尔经济学奖得主克莱夫·格兰杰[13]提出的，它是验证时间序列变量间是否存在因果关系的计量经济模型。格兰杰因果检验的前提条件是时间序列必须具有平稳性和变量间的协整性，否则可能会出现虚假回归问题。因此，在进行格兰杰检验之前，首先对各时间序列数据的平稳性进行单位根检验(Unit Root Test)。

      2.2.1 数据的单位根(ADF)检验

      本文用增广迪基—富勒检验法(ADF检验)对天津和上海两市的物流指标和经济发展数据进行单位根(ADF)检验，以此来判断生产总值对数值、物流业产值对数值、物流产业投资对数值、物流里程对数值、货物周转量对数值的平稳性，检验结果见表1。