云南省图书馆机构用户,欢迎您!
根据传统的T.T.T.理论,在假设温度不变的条件下,推导出食品的腐败率与时间的非线性关系,并在此基础上建立了惩罚函数和冷链物流节点选址模型。采用遗传算法对模型进行求解,通过一个算例证明了遗传算法可以有效解决冷链物流节点选址问题。


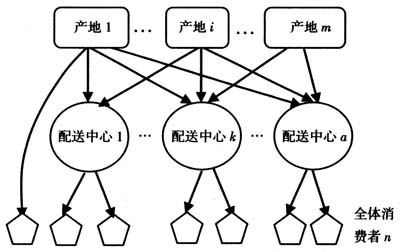 图1 冷链物流网络拓扑结构 给定某一地区所有需求点(用户)的地址集合,要求从中选出一定数目的地址建立配送中心,从而建立一系列的配送区域,实现各个需求点的配送,使得在选出点建立的配送中心与各需求点形成的配送系统总配送费用最少。为了便于建立模型,作一定的假设,假设系统满足如下条件:①仅在一定的被选范围内考虑设置新的配送中心;②运输费用与运量成正比;③产品从工厂到用户的运输和仓储过程中温度保持不变;④一个需求点仅由一个配送中心或工厂供应;⑤配送中心容量可以满足需求;⑥各资源厂的供给量和各需求点的需求量一定且为已知;⑦所有点间运输速度一样,均为常数。模型如下
图1 冷链物流网络拓扑结构 给定某一地区所有需求点(用户)的地址集合,要求从中选出一定数目的地址建立配送中心,从而建立一系列的配送区域,实现各个需求点的配送,使得在选出点建立的配送中心与各需求点形成的配送系统总配送费用最少。为了便于建立模型,作一定的假设,假设系统满足如下条件:①仅在一定的被选范围内考虑设置新的配送中心;②运输费用与运量成正比;③产品从工厂到用户的运输和仓储过程中温度保持不变;④一个需求点仅由一个配送中心或工厂供应;⑤配送中心容量可以满足需求;⑥各资源厂的供给量和各需求点的需求量一定且为已知;⑦所有点间运输速度一样,均为常数。模型如下 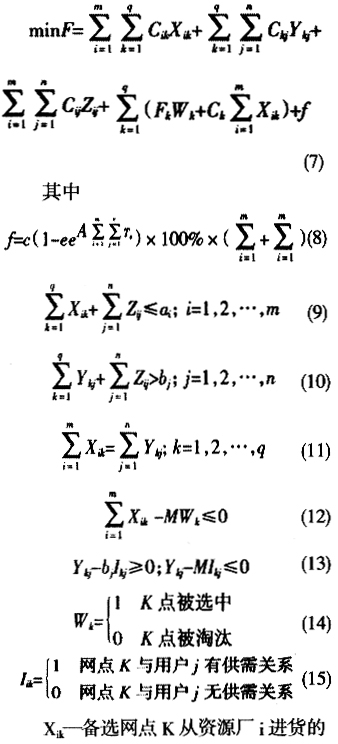
 5 模型求解 上述问题属于大规模冷链物流网络设计问题,分为两个子问题,配送中心的选址问题和根据就近原则对客户进行分派,具有NP-Hard性质,本文采用遗传算法来求解,通过Matlab编程来实现,其算法流程,如图2所示。 1)二进制编码。染色体的基因位数为待选配送中心位置数。若基因位的值为0,则表示该位置未被选中;若基因位的值为1,则表示该位置被选中。 2)初始化。包括选址的初始化和在选址条件下的分派优化问题。在第i个染色体中,从k个待选地中随机选择2或3个配送中心,然后采用就近原则把客户分派给选中的配送中心或工厂。并保证配送中心的流入量等于流出量。 3)计算适应度值。适配值函数用于对各状态的目标值作适当的变换,用以体现各状态性能的差异。本文采用总物流费用作为适应度值进行评价,即用式(7)计算,相关的系数由费用计算公式和统计数据获得。
5 模型求解 上述问题属于大规模冷链物流网络设计问题,分为两个子问题,配送中心的选址问题和根据就近原则对客户进行分派,具有NP-Hard性质,本文采用遗传算法来求解,通过Matlab编程来实现,其算法流程,如图2所示。 1)二进制编码。染色体的基因位数为待选配送中心位置数。若基因位的值为0,则表示该位置未被选中;若基因位的值为1,则表示该位置被选中。 2)初始化。包括选址的初始化和在选址条件下的分派优化问题。在第i个染色体中,从k个待选地中随机选择2或3个配送中心,然后采用就近原则把客户分派给选中的配送中心或工厂。并保证配送中心的流入量等于流出量。 3)计算适应度值。适配值函数用于对各状态的目标值作适当的变换,用以体现各状态性能的差异。本文采用总物流费用作为适应度值进行评价,即用式(7)计算,相关的系数由费用计算公式和统计数据获得。 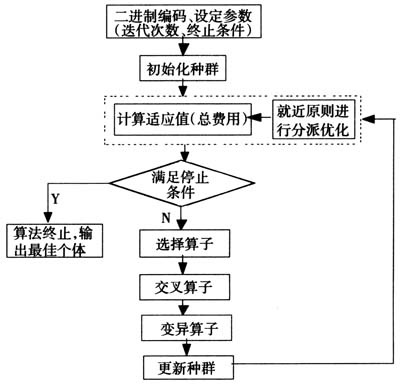 图2 GA方法求解程序 4)选择算子。选择操作是建立在群体中个体的适应度评估基础上的,适应度值越小,该个体被遗传到下一代群体中的概率也就越大。本文采用精英法进行染色体的选择,即将上一代中最好的一个或多个个体直接加入下一代中。再按轮盘赌方式进行选择,这样可以保证遗传算法的收敛性。
图2 GA方法求解程序 4)选择算子。选择操作是建立在群体中个体的适应度评估基础上的,适应度值越小,该个体被遗传到下一代群体中的概率也就越大。本文采用精英法进行染色体的选择,即将上一代中最好的一个或多个个体直接加入下一代中。再按轮盘赌方式进行选择,这样可以保证遗传算法的收敛性。