欧元区银行利率传导：基于对主要成员国的实证分析

      货币金融中介(银行)在货币政策传导中的作用不仅体现在银行信贷供给上，也体现在其对货币政策利率调整的反映速度和程度上。一般地，中央银行的货币政策行动是通过进行公开市场操作来实现政策利率预期目标，然后在金融市场上由政策利率首先传导到相关的短期市场利率并进一步传导到长期利率，由长期利率影响消费和投资。可见，银行利率对货币政策利率调整的速度和程度将影响到货币政策传导的有效性。这样，就可以通过衡量银行贷款和存款利率的调整速度和规模来反映市场利率对政策利率变动的反映。

      我们下面将运用向量自回归模型(VAR)以及向量误差校正模型(VECM)实证分析欧元区单一货币政策实施后，货币政策利率对主要欧元区成员国银行信贷和存款利率的传导机制。由于隔夜货币市场利率与政策利率高度相关，因此我们的实证分析中将隔夜货币市场利率作为货币政策利率的代理变量。

      一、传导模型

      Borio和Fritz(1995)、Cottarelli和Kourelis(1994)对短期银行信贷利率传导进行了国别比较研究。他们通过对样本中的欧元区国家进行研究，发现除芬兰和法国外，其他欧元区国家利率传导的长期弹性十分相似，并且利率传导的调整大多在6个月就完成。与他们相似地，我们运用误差修正模型(ECM)对欧元区主要国家的银行零售利率传导进行对比研究，模型具体形式如下：

      

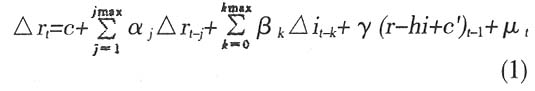      其中r和i分别代表银行利率以及隔夜货币市场利率，△表示一阶差分变换，j和k表示相应变量的滞后期数。与简单OLS回归相比较，误差修正模型有较好的经济解释。当△r=△i=0时，能够得到长期均衡方程r=hi+c′。因此误差修正模型实际上描述了变量向长期均衡状态调整的非均衡动态调整过程，其中(r-hi+c′)[，t-1]表示上一期变量偏离均衡状态的误差，这就是误差修正项。γ为修正系数，表示误差修正项对△r[，t]的修正速度，其符号应当为负，表明误差修正机制是一个负反馈系统。当变量之间存在协整关系时，系数γ在统计上将是显著性的，它允许内生变量偏离均衡路径时通过一系列局部短期调整而逐渐校正回到均衡路径。

      与Borio等人的研究不同，Angeloni等(2003)运用简单的OLS回归估计隔夜货币市场利率对于银行利率传导的效应，模型具体如下：

      

      由于在利用误差修正模型进行间归时，如果变量之间的协整关系不存在，那么误差修正机制就不复存在，误差修正模型相应地也变得没有意义。因此，我们在利用误差修正模型进行回归的同时，也相应地进行简单OLS回归，以对回归结果进行对比。

      二、数据来源和变量说明

      我们的研究主要包括六个核心欧元区成员国，它们分别是比利时、德国、西班牙、法国、意大利和荷兰。由于这六大成员国的经济产出占区内总产出的80％以上，因此对它们银行利率传导的事实进行实证分析将具有很强的代表性。与以往的研究不同(Mojon,2000; Angeoloni,2003)，我们的实证分析集中在单一货币政策推行后的银行利率传导事实上，这样一方面可以排除利率传导中货币政策效用函数和决策机制不同带来的差异性，另一方面也有助于我们考察单一货币政策推行以采成员国利率传导是否存在差异。

      与Mojon(2000)一样，我们选取欧元区隔夜货币市场利率作为货币政策利率的代理变量。另外，我们将对银行利率传导的分析集中在5大零售利率的分析上，它们分别是抵押贷款利率、企业短期借贷利率、企业投资信贷利率、定期存款利率以及储蓄存款利率。

      值得注意的是，对各银行利率工具的定义是基于各成员国的各自定义的基础之上的，这意味着不同成员国同一利率工具可能在定义上会存在有细微的差别①。尽管如此，我们认为利用各国各自定义的利率工具仍然具有重要的意义和启示。这主要是由于各国的定义反映了特定利率工具在其国内的使用程度，从而本身可以反映各成员国在金融结构上存在的差异。

      我们的回归分析采用月度数据，各国回归的样本区间略有不同。其中，荷兰、比利时、意大利和法国的样本区间为1999年的1月到2003年的9月；德国为1999年1月到2003年6月；西班牙为1999年1月到2003年3月。之所以没有包括更近的利率时间序列并进行分析，主要是由于我们所有的数据均来自于欧洲中央银行网站(ECB)，而ECB对利率工具各国的最近统计在2003年就截至了。虽然欧盟统计局网.站对2003年区内主要成员国的利率工具进行了统计，但统计口径与ECB提供的数据差异性很大，不能直接与从ECB得到的数据进行合并和分析。