云南省图书馆机构用户,欢迎您!
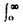 (1-k)f(y-z)N(y)dy(2) 其中,N(y)是收入为y的消费单位数,Y为总可支配收入。 根据假定x≥0,f(0)=1,(2)式可改写为: APC=k+(1-k)(z/
(1-k)f(y-z)N(y)dy(2) 其中,N(y)是收入为y的消费单位数,Y为总可支配收入。 根据假定x≥0,f(0)=1,(2)式可改写为: APC=k+(1-k)(z/ )+(1-k)
)+(1-k)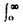 (x/
(x/ )f(x)n(x)dx(3) 其中,
)f(x)n(x)dx(3) 其中, =Y/N人均可支配收入,n(x)=N(x)/N拥有超额收入x的比例,进一步改写(3)式得: APC=k+(1-k)(z/
=Y/N人均可支配收入,n(x)=N(x)/N拥有超额收入x的比例,进一步改写(3)式得: APC=k+(1-k)(z/ )+(1-k)(1-z/
)+(1-k)(1-z/ )
)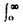 (x/
(x/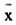 )f(x)n(x)dx(4) 令F(t)=
)f(x)n(x)dx(4) 令F(t)=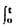 n(x)dx为超额收入x≤t的累积人口比例,令F[,1](t)=
n(x)dx为超额收入x≤t的累积人口比例,令F[,1](t)=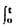 (x/
(x/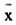 )n(x)dx表示超额收入x≤t的个体所得到的累积收入比例,再令F[,2](t)=
)n(x)dx表示超额收入x≤t的个体所得到的累积收入比例,再令F[,2](t)=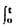 (x/
(x/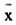 )f(x)n(x)dx表示超额收入x≤t的个体所消费的累积比例;则F(t),F[,1](t)、F[,2](t),F(t)可以在Lorenz收入——消费分配曲线中表示(见图1)。 Lorenz收入——消费分配曲线 附图
)f(x)n(x)dx表示超额收入x≤t的个体所消费的累积比例;则F(t),F[,1](t)、F[,2](t),F(t)可以在Lorenz收入——消费分配曲线中表示(见图1)。 Lorenz收入——消费分配曲线 附图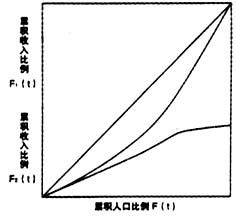 在图1中,因为f(x)≤1,所以,F[,2](t)≤F[,1](t)对于所有的t都成立,若f(x)<0意味着严重不均。F[,2](t),F(t)决定的曲线位于F(t),F[,1](t)曲线的下方,F[,2]=lim[,t]→∞F[,2](t)式(4)式的积分区间,此积分为超额收入中用来消费的比例。同样,根据f(x)≤1还可以得到,F[,2] (t),F(t)曲线的斜率小于F(t),F[,1](t)曲线的斜率,进一步,如果我们假设x服从窄尾分布,xf(x)n(x)就变得非常小,这样,F(t),F[,2](t)曲线的斜率将会降低到零,而F(t),F[,1](t)曲线的斜率则一直上升。这意味着积分F[,2](代表收入分配对消费倾向的影响)随基尼系数上升而下降。 总收入、超额收入的基尼系数之间的关系
在图1中,因为f(x)≤1,所以,F[,2](t)≤F[,1](t)对于所有的t都成立,若f(x)<0意味着严重不均。F[,2](t),F(t)决定的曲线位于F(t),F[,1](t)曲线的下方,F[,2]=lim[,t]→∞F[,2](t)式(4)式的积分区间,此积分为超额收入中用来消费的比例。同样,根据f(x)≤1还可以得到,F[,2] (t),F(t)曲线的斜率小于F(t),F[,1](t)曲线的斜率,进一步,如果我们假设x服从窄尾分布,xf(x)n(x)就变得非常小,这样,F(t),F[,2](t)曲线的斜率将会降低到零,而F(t),F[,1](t)曲线的斜率则一直上升。这意味着积分F[,2](代表收入分配对消费倾向的影响)随基尼系数上升而下降。 总收入、超额收入的基尼系数之间的关系