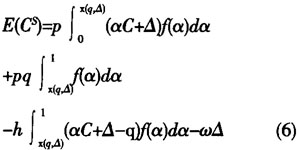1 引言 近年来,供应链协同管理成为供应链管理领域研究的热点[1,2]。而生产商与供应商之间的协同是供应链协同管理研究的重点问题[3,4]。Monahan第一个考虑了只有一个供应商和一个生产商的二级供应链系统通过数量折扣来实现协同的问题,他从供应者的观点研究了双方之间通过产品数量折扣来增加双方利润[5];Corbett和Groote在此基础上又得出了不对称信息下双方之间的最佳数量折扣[6]。而近两年来,有关供应链合约的研究增多,Porteus和Whang研究了在多产品经销模型下具有不对称信息的多代理商和一家制造业公司的协同问题,他们提出了使企业的预期收益最大的合约激励方案[7]。另外,Reyniers和 Tapiero研究了生产商与供应商之间如何通过合约的制定来实现产品品质的保证[8],Aderohumu和Mobolurin研究了生产商与供应商之间为了保证准时生产的顺利实施针对产品准时交付的合约制定问题[9]。然而,目前关于合约制定的研究文献主要强调的仍然是在一个理论代理框架下的问题,分析合约是否可以应用于一个分散系统的文献较少。 对于分散系统协同问题的研究, Christoph和Zimmer研究了基于二层规划的供应链协同机制[10]。分析了在供应链内部各自拥有私有信息的情况下通过综合使用“任务”导向和“控制”导向策略来实现生产商与供应商之间的协同运作问题,这里任务导向策略指生产商对零件订货量的最优决策,而控制导向策略指未满足订单情况下生产商关于惩罚成本的最优决策。在上述研究的基础上,Zimmer应用运筹学的最优化方法进一步建立了关于惩罚和奖励两种激励方式分别与订货量相结合的协同机制,并分别确定了惩罚成本与订货量、奖金与订货量的最优组合值[11]。另外,卢震和黄小原提出了一种具实际意义的供应链协调机制——Stackelberg主从对策,推导了Stackelberg均衡解[12]。 本文在文献[11]的基础上,建立了生产商与供应商的预期成本和预期利润函数,通过对信息隐匿和信息对称两种情况的比较,分析了建立协同机制的必要性。与文献[11]不同的是,同时引进了基于惩罚和奖励的激励函数,提出了由订货量、奖金和惩罚成本三种激励方式相结合的协同机制,着重研究了订货量一定的情况下,生产商通过对惩罚成本和奖金的调整使非对称信息下供应链系统的绩效实现最优的问题,并进行了仿真计算,确定了惩罚成本和奖金的最优组合值。 2 基本模型 这里考虑的是包含一个供应商和一个生产商的二级供应链系统。供应商正常的供应能力为C,供应商满足特定生产商的供应能力表示为αC(α∈[0,1])。生产商在发出订单之时,供应商并不能确定α的值(因为需要等待其它生产商的订单),故α为随机变量,仅知道它的概率密度函数f(α)。即所研究供应链的供应量是不确定的(假设供应时间确定,满足及时交付)。 为了更好满足订单需求,供应商针对特定的生产商还要建立一个额外供应量△。则交货量d的确定主要是根据随机供应量αC,额外供应量△和订货量q。即交货量满足 d≤αC+△(1) 且供应商的交货量不会大于订单要求的订货量,所以交货量为 d=min{αC+△,q}(2) 2.1 生产商模型 根据文献[11],生产商关于交货量d的实际成本函数为:
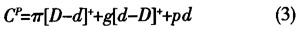
式(3)中,
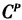
是生产商总成本;π为产成品的单位缺货成本;D是产品的外部需求;d是交货量;g是单位零件的库存成本;p是单位零件的购买成本。 生产商的预期总成本函数为

2.2供应商模型 根据文献[11],供应商实际利润函数为
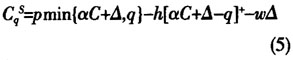
式(5)中,
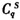
为供应商利润;p为零部件价格;C是正常供应能力;α是正常供应能力的随机比例;△是额外供应量;q是订货量;h为单位产品的持有成本;ω为单位零件购买成本。 供应商的预期利润函数为
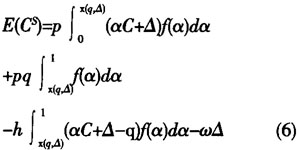
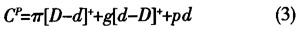 式(3)中,
式(3)中,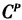 是生产商总成本;π为产成品的单位缺货成本;D是产品的外部需求;d是交货量;g是单位零件的库存成本;p是单位零件的购买成本。 生产商的预期总成本函数为
是生产商总成本;π为产成品的单位缺货成本;D是产品的外部需求;d是交货量;g是单位零件的库存成本;p是单位零件的购买成本。 生产商的预期总成本函数为  2.2供应商模型 根据文献[11],供应商实际利润函数为
2.2供应商模型 根据文献[11],供应商实际利润函数为 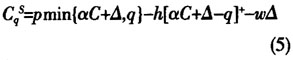 式(5)中,
式(5)中,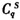 为供应商利润;p为零部件价格;C是正常供应能力;α是正常供应能力的随机比例;△是额外供应量;q是订货量;h为单位产品的持有成本;ω为单位零件购买成本。 供应商的预期利润函数为
为供应商利润;p为零部件价格;C是正常供应能力;α是正常供应能力的随机比例;△是额外供应量;q是订货量;h为单位产品的持有成本;ω为单位零件购买成本。 供应商的预期利润函数为