云南省图书馆机构用户,欢迎您!
本文评估最近文献中两个对现代汉语“都”的非全称量化的解释方案,包括“都”作为由“汇聚”义动词演化而来的程度/语力加强词的分析,以及“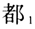 ”向右无量化的观点。本文指出,这两个解释方案均不能证明汉语“都”不是全称量化词。基于汉英全称量化的对比,本文揭示自然语言全称量化并非不能存在例外。同时,汉语“都”和表例外短语共现时,只能推出剔除例外成分而相减的语义,则从侧面证明“都”具备全称量化力。而副词“几乎”能与“都”共现则进一步支持“都”是全称量化词。最后,文章讨论文献中提到的三个句法语义证据,都证明汉语“都”本质上是一个关联方向敏感的全称量化词:1)“都”与疑问代词的交互作用;2)只有“都”的限定域允准极项敏感词;3)“都”的左向穷尽性与右向排他性分野。
”向右无量化的观点。本文指出,这两个解释方案均不能证明汉语“都”不是全称量化词。基于汉英全称量化的对比,本文揭示自然语言全称量化并非不能存在例外。同时,汉语“都”和表例外短语共现时,只能推出剔除例外成分而相减的语义,则从侧面证明“都”具备全称量化力。而副词“几乎”能与“都”共现则进一步支持“都”是全称量化词。最后,文章讨论文献中提到的三个句法语义证据,都证明汉语“都”本质上是一个关联方向敏感的全称量化词:1)“都”与疑问代词的交互作用;2)只有“都”的限定域允准极项敏感词;3)“都”的左向穷尽性与右向排他性分野。
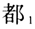 ”、表“甚至”的“
”、表“甚至”的“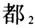 ”以及表“已经”的“
”以及表“已经”的“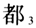 ”。在形式句法语义研究中,“都”被分析为全称量化词(Lee 1986;蒋严1998;潘海华2006;蒋静忠、潘海华2013;冯予力、潘海华2018),加合算子(sum operator)(Huang 1996;袁毓林2005),分配算子(distributor)(Lin 1998),最大化算子(maximizer)(Giannakidou and Cheng 2006;Xiang 2008),程度/语力加强词(吴义诚、周永2019;周永、吴义诚2020)。在选项语义学(alternative semantics)框架中,“都”相当于抽象的EVEN(Liu 2017)或一个预穷尽化的穷尽性算子(pre-exhaustification exhaustifier)(Xiang 2020)①。 本文首先简要介绍最近文献中两个对现代汉语“都”的非全称量化的解释方案,包括将“都”分析为由“汇聚”义动词演化而来的程度/语力加强词(吴义诚、周永2019),以及“
”。在形式句法语义研究中,“都”被分析为全称量化词(Lee 1986;蒋严1998;潘海华2006;蒋静忠、潘海华2013;冯予力、潘海华2018),加合算子(sum operator)(Huang 1996;袁毓林2005),分配算子(distributor)(Lin 1998),最大化算子(maximizer)(Giannakidou and Cheng 2006;Xiang 2008),程度/语力加强词(吴义诚、周永2019;周永、吴义诚2020)。在选项语义学(alternative semantics)框架中,“都”相当于抽象的EVEN(Liu 2017)或一个预穷尽化的穷尽性算子(pre-exhaustification exhaustifier)(Xiang 2020)①。 本文首先简要介绍最近文献中两个对现代汉语“都”的非全称量化的解释方案,包括将“都”分析为由“汇聚”义动词演化而来的程度/语力加强词(吴义诚、周永2019),以及“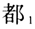 ”向右无量化的观点(周韧2021)。然后,反驳他们对现代汉语“都”的非全称量化的解释,指出这两个解释方案均不能证明汉语“都”不是全称量化词。我们提供更多的汉英全称量化的对比,以揭示自然语言全称量化并非不能存在例外。同时,汉语“都”和表例外短语共现时只能推出剔除例外成分的语义,这从侧面证明“都”具备全称量化力。最后,文章讨论文献中观察到的三个句法语义证据,包括:1)“都”与疑问词的交互作用,2)只有“都”的限定域允准极项敏感词,以及3)“都”的左向穷尽性与右向排他性分野,证明“都”本质上是一个关联方向敏感的全称量化词。 2.“都”非全称量化的最新解释 2.1 “都”为由“汇聚”义动词演化而来的程度/语力加强词 吴义诚、周永(2019)认为“都”并非真正的全称量化词,因为“都”可以与其他表全量的限定词“所有、每”或副词“全”共现。(1)表明,如果“都”是全称量化词,那么共现的限定词“所有”和副词“全”也可以视为全称量化词,这意味着需要对主语“学生”的集合进行多次量化,违反逻辑语义学的双射原则,即一个量化算子只能对应一个变量。同时,吴义诚、周永(2019)指出,若将“都”分析为全称量化词,很难解释为什么(2)中的“都”需要和“每”共现。
”向右无量化的观点(周韧2021)。然后,反驳他们对现代汉语“都”的非全称量化的解释,指出这两个解释方案均不能证明汉语“都”不是全称量化词。我们提供更多的汉英全称量化的对比,以揭示自然语言全称量化并非不能存在例外。同时,汉语“都”和表例外短语共现时只能推出剔除例外成分的语义,这从侧面证明“都”具备全称量化力。最后,文章讨论文献中观察到的三个句法语义证据,包括:1)“都”与疑问词的交互作用,2)只有“都”的限定域允准极项敏感词,以及3)“都”的左向穷尽性与右向排他性分野,证明“都”本质上是一个关联方向敏感的全称量化词。 2.“都”非全称量化的最新解释 2.1 “都”为由“汇聚”义动词演化而来的程度/语力加强词 吴义诚、周永(2019)认为“都”并非真正的全称量化词,因为“都”可以与其他表全量的限定词“所有、每”或副词“全”共现。(1)表明,如果“都”是全称量化词,那么共现的限定词“所有”和副词“全”也可以视为全称量化词,这意味着需要对主语“学生”的集合进行多次量化,违反逻辑语义学的双射原则,即一个量化算子只能对应一个变量。同时,吴义诚、周永(2019)指出,若将“都”分析为全称量化词,很难解释为什么(2)中的“都”需要和“每”共现。  此外,吴义诚、周永(2019)认为,将“都”分析为分配算子、加合算子或者最大化算子都不能揭示其本质语义。比如下例,对于分配性谓词“睡”来讲,“都”出现与否都不影响句子获得分配性解读,因此分配性应该不是“都”的本质语义。
此外,吴义诚、周永(2019)认为,将“都”分析为分配算子、加合算子或者最大化算子都不能揭示其本质语义。比如下例,对于分配性谓词“睡”来讲,“都”出现与否都不影响句子获得分配性解读,因此分配性应该不是“都”的本质语义。  为了解释(2)中“都”和“每”共现时的语义,Huang(1996)和袁毓林(2005)指出,“都”是针对事件的加合算子,将“每”分配的个体事件加合成为一个复数事件。与熊仲儒(2016)一样,吴义诚、周永(2019)对“都”能够加合个体事件持怀疑态度。他们指出,(4)中“都”的作用对象并非明确要求存在个体或复数,因为主语是不可数名词,很难找到一个复数的、由不可数名词构成的事件集合。
为了解释(2)中“都”和“每”共现时的语义,Huang(1996)和袁毓林(2005)指出,“都”是针对事件的加合算子,将“每”分配的个体事件加合成为一个复数事件。与熊仲儒(2016)一样,吴义诚、周永(2019)对“都”能够加合个体事件持怀疑态度。他们指出,(4)中“都”的作用对象并非明确要求存在个体或复数,因为主语是不可数名词,很难找到一个复数的、由不可数名词构成的事件集合。 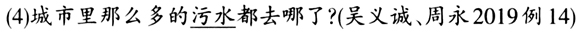 此外,吴义诚、周永(2019)认为将“都”分析为最大化算子也有一定的问题。基于Giannakidou和Cheng(2006),Xiang(2008)主张“都”的全称量化以及“甚至”义都由“都”作为最大化算子推衍而来。比如,在“学生都来了”中,“都”作为最大化算子选择由学生构成的集合中最大的复数个体,从而推出“都”的全称量化义。而“都”表“甚至”的解读来自于“都”作用于一个由程度组成的量级。比如在(5)中,“都”得出主语最大的生气程度。
此外,吴义诚、周永(2019)认为将“都”分析为最大化算子也有一定的问题。基于Giannakidou和Cheng(2006),Xiang(2008)主张“都”的全称量化以及“甚至”义都由“都”作为最大化算子推衍而来。比如,在“学生都来了”中,“都”作为最大化算子选择由学生构成的集合中最大的复数个体,从而推出“都”的全称量化义。而“都”表“甚至”的解读来自于“都”作用于一个由程度组成的量级。比如在(5)中,“都”得出主语最大的生气程度。