2022年4月,《中共中央、国务院关于加快建设全国统一大市场的意见》公布,提出打造统一的要素和资源市场,包括健全城乡统一的土地和劳动力市场、加快发展统一的资本市场、加快培育统一的技术和数据市场、建设全国统一的能源市场以及培育发展全国统一的生态环境市场。其中,能源市场和生态环境市场均与“双碳”目标紧密相关。低碳转型是现阶段我国经济社会发展、转型的必经之路,不同于发达国家的低碳转型路径,我国的低碳转型需要在实现节能减排的过程中,满足不断扩张的能源需求。然而,在“双碳”目标的驱动下,仍存在部分企业对碳排放数据进行修改甚至伪造的舞弊行为,进而打破碳市场规则、扰乱碳市场正常秩序,严重危害碳市场健康运行,阻碍“双碳”目标的顺利实现。 碳排放审计又称碳审计,它不是简单的财务审计、合规审计,而是一种应对碳减排工作的多元且复杂的审计,是环境审计的子项,也是环境审计工作新的指向。作为一种为改善生态环境而控制碳排放量的管理工具,碳排放审计为我国低碳经济的发展提供了一套切实可行的监督约束机制。随着碳排放审计理论与实践的发展,以英国为代表的部分发达国家早已实施了碳排放审计,例如,在2009年,英国环境审计委员会(EAC)针对碳的收集与储存、碳交易市场、碳收支等诸多低碳问题提出了进行全面审计的工作报告,成为全面碳审计的应用典范;同年,作为碳审计实践较早的国家之一,美国国家审计署也发布报告指出对汽车、房产和生活方式进行审计,抓住了碳审计重点,进而增强了人民的低碳意识。然而,在大数据时代下,传统的数据采集、处理和分析应用方法,已难以适应海量的碳排放审计数据环境,若碳排放审计人员继续按照传统审计方法进行碳排放审计,不仅无法充分挖掘审计数据的潜在价值,而且使得审计风险大大增加,甚至导致审计失败。因此,如何在海量的多源、多维、异构审计数据中,充分利用审计数据的大集中、大综合、大关联的特征,促进审计人员形成用数据说话、用数据决策的大数据审计思维,实现碳排放审计疑点的精准定位,加强审计力度、优化审计方法、提高审计效率,已成为碳排放审计面临的迫切要求和全新挑战。 基于此,部分学者提出,通过在审计工作中引入大数据技术,例如机器学习、数据挖掘等方法辅助审计活动的开展,从而提升审计效率。机器学习是一个多学科交叉研究领域,包括计算机学科、概率统计学科等,其利用计算机对现有数据进行学习并产生反映数据关联的模型从而辅助判断与决策。机器学习按照对不同数据的处理方式,一般可分为监督学习、半监督学习、无监督学习以及强化学习。作为无监督学习的一种,K-Means聚类算法通过迭代求解,能够在无任何先验知识的情况下发掘数据的相似性,进而实现数据分组的目的。因此,基于K-Means聚类算法的思想简单、聚类效果优、可解释性强等优点,受到了学者的广泛关注。杨蕴毅等运用迭代式聚类的方法,以上市公司财务数据为样本,利用证监会等机构的非结构化数据,实现了审计疑点的迅速挖掘。WangXuren等针对用户异常数据库行为,采用K-Means聚类方法对其进行分组,大幅度提高了数据库泄露风险的检测效率与精确性。由此可见,K-Means聚类方法有助于应对大数据中的异常问题,并且对审计疑点的迅速发现与确认有着独特的天然技术优势。 本文在对已有文献的整理和分析的基础上,说明了K-Means聚类算法在审计工作中能够具有独特优势,为“机器学习+碳排放审计”的研究提供了相应理论依据。基于此,本文从当前传统碳排放审计中存在的问题出发,创造性地将机器学习中的K-Means聚类算法与碳排放审计相结合,构建了碳排放审计预警框架,在降低审计成本的同时,兼顾了审计效率,最后以H企业碳排放审计预警为例进行仿真,表明基于机器学习K-Means聚类算法的碳排放审计预警系统的可行性,进一步推动了碳排放审计的发展。 二、K-Means聚类算法 K-Means算法是当前最为流行的聚类算法模型之一,主要通过逐步迭代优化聚类结果,同时不断地将目标数据集重新分配到每个聚类中,从而被广泛应用于数据处理、图像识别、市场分析和风险评估等研究领域。其主要步骤如下: 步骤(1):随机地从N个样本数据中选择K个对象,其中每个对象均代表一个簇的初始均值或质心; 步骤(2):对剩余的对象,根据其到每个簇均值的欧氏距离,将其分配到距离最近的簇中; 步骤(3):使用每个聚类中的样本均值作为新的质心。 接下来,依次重复步骤(2)和(3)直到簇的均值不再发生变化,聚类中心不再改变。
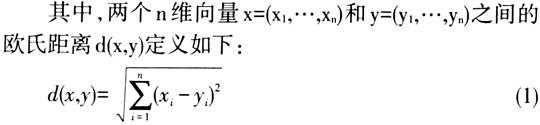
K-Means聚类算法评价准则之一是误差平方和准则,误差平方和简称为SSE,其定义如下:

其中,k为簇的个数,
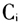
为第i簇,p为某个簇中任意一点,
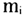
为簇
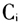
的均值。SSE值越小,说明数据点越接近质心,聚类效果则越好;反之,若SSE越大,聚类效果则越差,多个聚类被视为一个聚类的可能性就越大。因此,在聚类过程中需要将误差平方和较大的聚类再次进行划分。
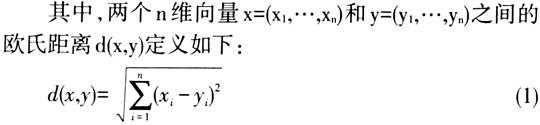 K-Means聚类算法评价准则之一是误差平方和准则,误差平方和简称为SSE,其定义如下:
K-Means聚类算法评价准则之一是误差平方和准则,误差平方和简称为SSE,其定义如下:  其中,k为簇的个数,
其中,k为簇的个数,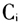 为第i簇,p为某个簇中任意一点,
为第i簇,p为某个簇中任意一点,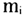 为簇
为簇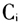 的均值。SSE值越小,说明数据点越接近质心,聚类效果则越好;反之,若SSE越大,聚类效果则越差,多个聚类被视为一个聚类的可能性就越大。因此,在聚类过程中需要将误差平方和较大的聚类再次进行划分。
的均值。SSE值越小,说明数据点越接近质心,聚类效果则越好;反之,若SSE越大,聚类效果则越差,多个聚类被视为一个聚类的可能性就越大。因此,在聚类过程中需要将误差平方和较大的聚类再次进行划分。