考试是评价教学效果的最佳手段,评价的最高境界是教、学、评高度一致.所谓教、学、评一致性是指教师的教、学生的学以及对教与学的考核评价统辖在统一的标准之下,三者具有高度的相关性.具体地讲,就是教什么、学什么、考什么是一致的;怎么教、怎么学、怎么评是一致的;教到什么程度、学到什么程度、考到什么程度是一致的;教学设计、教学实施、教学效果是一致的.2019年12月江苏省南京市5所高中进行联合阶段检测,高一数学学科命题组委托笔者命制一道压轴题.本文就教、学、评一致性视角下的考题命制过程谈谈个人的感受与思考,不足之处请广大同行批评指正. 一、命题准备 (一)考什么 命题前首先对主要知识点、思想方法、能力考查进行梳理.本次阶段检测的命题范围:高中《数学(必修1)》全部内容和《数学(必修4)》第一章“三角函数”.本部分重点内容是基本初等函数:二次函数、指数与对数函数、三角函数.常见考查点有:定义域、值域、单调性、奇偶性、周期性、指数对数的运算、零点等,以函数知识为载体的思想方法有数形结合、函数与方程、转化与化归、分类讨论、换元法等等[1].对能力的考查主要有:运算能力、推理能力、转化能力.压轴题应重在考查学生综合运用知识解决问题的能力.但对于高一学生来说,注重基本概念、基本方法和通性通法的考查仍是命题的重点,应在此基础上适当增加题目的区分度. (二)怎么考 考试的目的一方面是对前一阶段学习的反馈,更重要的是能启发学生反思前一阶段的学习,进而调整优化后阶段的学习,最终以提高学生的元认知能力为终极目标.题目太难了,学生会质疑平时的教学与学习,让学生失去学习的方向,进而失去兴趣,失去信心;题目太容易了,学生会轻视数学学习.因此,“教什么、学什么、考什么”要一致,作为压轴题还要保持适当的难度和区分度. 笔者研究了近几年的江苏省数学高考题和各大市高一期末考试试题发现,多数压轴题均以新定义题的形式考查.新定义题既能兼顾基础知识方法的考查也能适当增加难度和区分度,命题弹性很大,这也是多数命题教师一向青睐这种题型的原因.对学生来说,新定义题题目新颖,读题能力要求自然就高,其本质上是在熟练知识的同时考查学生分析问题和转化问题的能力.鉴于函数知识的自身特点,若将参数范围、分类讨论、恒成立、存在性问题、整体换元等融入进去,则更能凸显对函数本质的考查,因此作为压轴题的函数题选用新定义题型更为合适. (三)寻求母题 完全创新难度比较大,寻找一道母题进行改编、迁移、创新是命题的基本途径,既要保证题目新颖也要确保难度适中,知识方法的考查不偏不怪.翻阅教材例习题、近几年江苏各大市的高一期末考试题和部分高三一轮复习题,一道“老题”让笔者眼前一亮,最终决定拿这道题“开刀”. 母题 对于函数f(x),若在定义域内存在实数x,满足f(-x)=-f(x),则称f(x)为“局部奇函数”. 1)已知二次函数
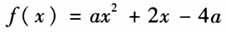
(其中a∈R),试判断f(x)是否为“局部奇函数”,并说明理由; 2)若f(x)=2x+m是定义在区间[-1,1]上的“局部奇函数”,求实数m的取值范围; 3)若
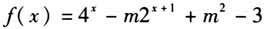
为定义域R上的“局部奇函数”,求实数m的取值范围. 仔细研究本题,笔者有3点启发:一是新定义题考查的一般特点为第1)小题对定义判定进行考查、第2)小题对定义性质进行考查、第3)小题考查含有参数的综合问题;二是以函数零点为载体能综合考查函数的基本性质;三是对典型数学思想方法的考查仍是命题的暗线. 同时笔者还发现两处不妥:一是对指数函数的考查过多;二是后面两个小题要用到基本不等式(或双勾函数)求范围,对高一学生来说显然超纲(虽然绝大多数教师已补充讲过双勾函数的相关性质,但不适合作为联考考题考查).这就迫使笔者对这道题动“大手术”,大刀阔斧地改,甚至变为一道原创题. 二、命题过程 (一)改编历程 最初想把“局部奇函数”的定义改为“局部偶函数”的定义,并尝试用几个函数代入,当运用新定义解题时发现两边常数项消掉了,显然不妥.为了解决这一矛盾,尝试在定义式右边增加一个可变系数k,并命名为“k阶局部奇函数”(至今不知这个定义命名是否妥当),并限制k为整数.同时k也可以控制题目的难度,于是题干就此确定: 题干 对于函数f(x),若在定义域内存在实数x,满足f(-x)=-kf(x),其中k为整数,则称函数f(x)为定义域上的“k阶局部奇函数”. 接下来是设置问题,依然按照考查新定义的判定、性质、综合问题的顺序进行设置.内容要涵盖三角函数、二次函数和指对函数(或其一),由于三角函数刚刚学习过,学生对三角函数的认识还不够深刻,应放在第1)小题考查,于是构造了简单函数f(x)=sinx+cosx,并设置自变量x的简单范围
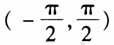
,判断f(x)是否为“二阶局部奇函数”.通过验证可得3sinx=cosx,存在实数x满足上式,笔者感觉这个问题设置还挺不错的.于是得到第1)小题:
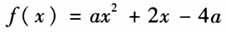 (其中a∈R),试判断f(x)是否为“局部奇函数”,并说明理由; 2)若f(x)=2x+m是定义在区间[-1,1]上的“局部奇函数”,求实数m的取值范围; 3)若
(其中a∈R),试判断f(x)是否为“局部奇函数”,并说明理由; 2)若f(x)=2x+m是定义在区间[-1,1]上的“局部奇函数”,求实数m的取值范围; 3)若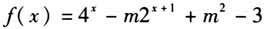 为定义域R上的“局部奇函数”,求实数m的取值范围. 仔细研究本题,笔者有3点启发:一是新定义题考查的一般特点为第1)小题对定义判定进行考查、第2)小题对定义性质进行考查、第3)小题考查含有参数的综合问题;二是以函数零点为载体能综合考查函数的基本性质;三是对典型数学思想方法的考查仍是命题的暗线. 同时笔者还发现两处不妥:一是对指数函数的考查过多;二是后面两个小题要用到基本不等式(或双勾函数)求范围,对高一学生来说显然超纲(虽然绝大多数教师已补充讲过双勾函数的相关性质,但不适合作为联考考题考查).这就迫使笔者对这道题动“大手术”,大刀阔斧地改,甚至变为一道原创题. 二、命题过程 (一)改编历程 最初想把“局部奇函数”的定义改为“局部偶函数”的定义,并尝试用几个函数代入,当运用新定义解题时发现两边常数项消掉了,显然不妥.为了解决这一矛盾,尝试在定义式右边增加一个可变系数k,并命名为“k阶局部奇函数”(至今不知这个定义命名是否妥当),并限制k为整数.同时k也可以控制题目的难度,于是题干就此确定: 题干 对于函数f(x),若在定义域内存在实数x,满足f(-x)=-kf(x),其中k为整数,则称函数f(x)为定义域上的“k阶局部奇函数”. 接下来是设置问题,依然按照考查新定义的判定、性质、综合问题的顺序进行设置.内容要涵盖三角函数、二次函数和指对函数(或其一),由于三角函数刚刚学习过,学生对三角函数的认识还不够深刻,应放在第1)小题考查,于是构造了简单函数f(x)=sinx+cosx,并设置自变量x的简单范围
为定义域R上的“局部奇函数”,求实数m的取值范围. 仔细研究本题,笔者有3点启发:一是新定义题考查的一般特点为第1)小题对定义判定进行考查、第2)小题对定义性质进行考查、第3)小题考查含有参数的综合问题;二是以函数零点为载体能综合考查函数的基本性质;三是对典型数学思想方法的考查仍是命题的暗线. 同时笔者还发现两处不妥:一是对指数函数的考查过多;二是后面两个小题要用到基本不等式(或双勾函数)求范围,对高一学生来说显然超纲(虽然绝大多数教师已补充讲过双勾函数的相关性质,但不适合作为联考考题考查).这就迫使笔者对这道题动“大手术”,大刀阔斧地改,甚至变为一道原创题. 二、命题过程 (一)改编历程 最初想把“局部奇函数”的定义改为“局部偶函数”的定义,并尝试用几个函数代入,当运用新定义解题时发现两边常数项消掉了,显然不妥.为了解决这一矛盾,尝试在定义式右边增加一个可变系数k,并命名为“k阶局部奇函数”(至今不知这个定义命名是否妥当),并限制k为整数.同时k也可以控制题目的难度,于是题干就此确定: 题干 对于函数f(x),若在定义域内存在实数x,满足f(-x)=-kf(x),其中k为整数,则称函数f(x)为定义域上的“k阶局部奇函数”. 接下来是设置问题,依然按照考查新定义的判定、性质、综合问题的顺序进行设置.内容要涵盖三角函数、二次函数和指对函数(或其一),由于三角函数刚刚学习过,学生对三角函数的认识还不够深刻,应放在第1)小题考查,于是构造了简单函数f(x)=sinx+cosx,并设置自变量x的简单范围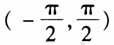 ,判断f(x)是否为“二阶局部奇函数”.通过验证可得3sinx=cosx,存在实数x满足上式,笔者感觉这个问题设置还挺不错的.于是得到第1)小题:
,判断f(x)是否为“二阶局部奇函数”.通过验证可得3sinx=cosx,存在实数x满足上式,笔者感觉这个问题设置还挺不错的.于是得到第1)小题: