一、U型教学模式的起源 数学的研究对象是抽象的,其学习过程也是一种抽象问题形象化、具体化的过程.特别是在呈现复杂的计算过程、函数图像的动态变化、几何图形的性质与判定、几何模型的结构时,常常会使用信息技术可视化手段.一般地说,数学虽然需要直观的观察,以具体的模型作为理解的基础,但是数学更多地要依靠抽象思维,概念最终需要抽象的概括,数学规律要求进行形式化的表达,证明必须符合抽象的逻辑推理.这往往又不是“视觉化”所能奏效的.有时不仅达不到提高课堂效率的效果,甚至会有一些负面作用,如影响学生对数学本质的认识,抑制学生思维的训练,阻碍学生数学理解能力的提高.这是教师们积极运用信息技术教学过程中经常出现的一种遗憾[1].由此可想,信息技术可视化课堂并不能停留在依赖信息技术手段体现的表面上的可视化功能,而是实实在在的把握教学可视化呈现的方式与时机.也就是说,在教学中运用信息技术可视化要着眼于提升学生的思维水平,使其从浅层学习向深度学习转化. 近十年来国际上最先进的教学理论其实根本不是国内的“翻转课堂”等技术性的策略,而是源于人工智能和脑科学的深度学习理论.深度学习注重让学生沉浸于知识的情境和学习的情境,强调批判性思维,注重实现知识的内在价值[2].我国学者黎加厚教授认为深度学习是指在理解学习的基础上,学习者能够批判性地学习新的思想和事实,并将它们融入原有的认知结构中,能够在众多思想间进行联系,能够将已有的知识迁移到新的情境中,做出决策和解决问题的学习[3].故此,高中数学信息技术可视化课堂要实现学生的深度学习,必须对学生学习过程进行关注.这就要求我们从深度学习向深度教学转向思考,怎样的可视化教学过程是符合学生的认知规律,有利于学生数学核心素养的培养,并具有高度的可操作性呢?其实从黎教授的观点不难看出,知识的学习需要经过还原与下沉、经验与探究、反思与上浮的过程,这也正好与美国著名教育家杜威的经验教学过程的理论相一致.这一过程恰似一个“U型”的过程(如下页图1).也就是说让学生历尽三个环节:(1)下沉——知识的内化与下沉;(2)潜行——再通过经验与探究,挖掘知识中的数学思想和方法;(3)上浮——最后才能达成知识的外化、迁移和运用.故此,要实现高中数学信息技术可视化的课堂应该是要遵循学生“U型学习”特点进行“U型教学”模式的构建.下沉:通过信息技术手段把外部信息、知识与学生内部知识结构建立联系,把抽象的、不可见的数学知识转化为可见的图形、图像、图表等.潜行:过程中要引导学生对所要探究的问题使用学科思想和方法做出更深层次的观察和思考.上浮:可以对所探究的问题进行自主总结,并提出新的猜想或假设,从而促进学生的深入思考、学习和数学学科核心素养的提升.很明显以上的这些思考都建立在教学过程的设计理念上,落实的关键就在于教学者.故此,下面以“与圆有关的最值问题”专题复习教学设计为例,谈谈如何在高中数学信息技术可视化课堂落实U型教学模式.

二、U型教学模式的落实 可视化变式教学强调通过保留命题图形本质特征和核心思想,合理改变可视化条件或问题的呈现形式,让学生多方位、多角度、深层次地理解图形或题目的本质属性,这对提高学生的思维能力和自主建构图形的能力有着显著作用,能够有效地体现新课程标准所提倡的从传统的“重结果”转变为“重过程”的教学思想[4].“与圆有关的最值问题”专题复习在用心打造的变式题组中,学生通过信息技术所带来的直观自主感知题中图形条件和问题的变化(下沉环节),对比不同的条件、不同的问题所呈现的图形,借助已有的数学思想和方法挖掘这些图形的共性和特点(潜行环节),并针对题目不同的变化能自主建构新问题(上浮环节).这何尝不是一个“U”型的学习过程? 教学场所:智慧教室,学生每人一部平板电脑. 教学工具:PPT,GeoGebra(下称GGB). 教学方法:由于整节课的核心图形都是一个以点(-2,3)为圆心,1为半径的圆.教师可以使用GGB把本课所需的基本图画好截图放在PPT上,课堂中可以使用电子白板在基本图中直接完成所有题目的作图变化.这样既减少课件间转换的时间,又减少课前软件的备课时间,更能体现出一图多变的可视化效果. 1.下沉环节:经典例题体验与内化 条件:已知点P(x,y)是圆
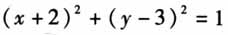
上的动点.

(4)

的最大值为________;最小值为________. (5)6x+8y的最大值为________;最小值为________. 解:(4)设A(1,2),可理解为求动直线AP斜率的最值问题,即转化为求切线斜率. (5)令z=6x+8y,则
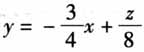
,可理解为求斜率为定值的平行直线的截距问题,即可转化为求切线的截距问题.
 二、U型教学模式的落实 可视化变式教学强调通过保留命题图形本质特征和核心思想,合理改变可视化条件或问题的呈现形式,让学生多方位、多角度、深层次地理解图形或题目的本质属性,这对提高学生的思维能力和自主建构图形的能力有着显著作用,能够有效地体现新课程标准所提倡的从传统的“重结果”转变为“重过程”的教学思想[4].“与圆有关的最值问题”专题复习在用心打造的变式题组中,学生通过信息技术所带来的直观自主感知题中图形条件和问题的变化(下沉环节),对比不同的条件、不同的问题所呈现的图形,借助已有的数学思想和方法挖掘这些图形的共性和特点(潜行环节),并针对题目不同的变化能自主建构新问题(上浮环节).这何尝不是一个“U”型的学习过程? 教学场所:智慧教室,学生每人一部平板电脑. 教学工具:PPT,GeoGebra(下称GGB). 教学方法:由于整节课的核心图形都是一个以点(-2,3)为圆心,1为半径的圆.教师可以使用GGB把本课所需的基本图画好截图放在PPT上,课堂中可以使用电子白板在基本图中直接完成所有题目的作图变化.这样既减少课件间转换的时间,又减少课前软件的备课时间,更能体现出一图多变的可视化效果. 1.下沉环节:经典例题体验与内化 条件:已知点P(x,y)是圆
二、U型教学模式的落实 可视化变式教学强调通过保留命题图形本质特征和核心思想,合理改变可视化条件或问题的呈现形式,让学生多方位、多角度、深层次地理解图形或题目的本质属性,这对提高学生的思维能力和自主建构图形的能力有着显著作用,能够有效地体现新课程标准所提倡的从传统的“重结果”转变为“重过程”的教学思想[4].“与圆有关的最值问题”专题复习在用心打造的变式题组中,学生通过信息技术所带来的直观自主感知题中图形条件和问题的变化(下沉环节),对比不同的条件、不同的问题所呈现的图形,借助已有的数学思想和方法挖掘这些图形的共性和特点(潜行环节),并针对题目不同的变化能自主建构新问题(上浮环节).这何尝不是一个“U”型的学习过程? 教学场所:智慧教室,学生每人一部平板电脑. 教学工具:PPT,GeoGebra(下称GGB). 教学方法:由于整节课的核心图形都是一个以点(-2,3)为圆心,1为半径的圆.教师可以使用GGB把本课所需的基本图画好截图放在PPT上,课堂中可以使用电子白板在基本图中直接完成所有题目的作图变化.这样既减少课件间转换的时间,又减少课前软件的备课时间,更能体现出一图多变的可视化效果. 1.下沉环节:经典例题体验与内化 条件:已知点P(x,y)是圆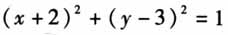 上的动点.
上的动点.  (4)
(4) 的最大值为________;最小值为________. (5)6x+8y的最大值为________;最小值为________. 解:(4)设A(1,2),可理解为求动直线AP斜率的最值问题,即转化为求切线斜率. (5)令z=6x+8y,则
的最大值为________;最小值为________. (5)6x+8y的最大值为________;最小值为________. 解:(4)设A(1,2),可理解为求动直线AP斜率的最值问题,即转化为求切线斜率. (5)令z=6x+8y,则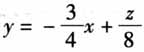 ,可理解为求斜率为定值的平行直线的截距问题,即可转化为求切线的截距问题.
,可理解为求斜率为定值的平行直线的截距问题,即可转化为求切线的截距问题.