云南省图书馆机构用户,欢迎您!
本文针对方言元音的性别变异问题,从声学角度分别对性别的生理差异与社会变异进行量化分析,侧重社会变异计算方法的探索。方法上通过计算生理归一化系数 来量化生理差异;通过对元音声学集中空间的归一化消减生理因素,再计算空间的面积与叠置率比较整体空间的社会变异,采用支持向量机方法对个体元音社会变异的强弱进行模式分析。实验结论主要有:生理归一化系数可以看作是元音的性别生理差异的尺度因子;社会变异分析的前提是选用适当的归一化方法消减生理差异,以得到社会变异的数据;整体上女性有更强的社会变异性,反映在女性声学空间的面积更大(4.475)、叠置率更小(0.712);模式检验说明,女性的前元音更趋前,后元音更趋后,空间边缘性更突出。
来量化生理差异;通过对元音声学集中空间的归一化消减生理因素,再计算空间的面积与叠置率比较整体空间的社会变异,采用支持向量机方法对个体元音社会变异的强弱进行模式分析。实验结论主要有:生理归一化系数可以看作是元音的性别生理差异的尺度因子;社会变异分析的前提是选用适当的归一化方法消减生理差异,以得到社会变异的数据;整体上女性有更强的社会变异性,反映在女性声学空间的面积更大(4.475)、叠置率更小(0.712);模式检验说明,女性的前元音更趋前,后元音更趋后,空间边缘性更突出。
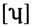 多见于男性,而少见于女性(吴波2017)。由于实验语音学的介入,方言语音的描写正逐渐走向新描写主义的精细化道路。目前有关汉语方言语音的性别变异一方面多限于描写性比较,对其计量方法的探索还存有空白;另一方面由于男女声带与声腔构造的差别,元音的生理差异易于解释,但其社会变异研究仍有待进一步深入。 有鉴于此,本文在新描写主义的背景下(胡建华2018),把性别变异分出生理差异与社会变异两种类型进行分析,拟讨论的问题主要有三:1)如何量化语音的生理差异尺度;2)在社会变异分析中如何消减生理因素的影响得到社会性数据;3)如何量化社会变异及其强弱。带着这些问题,下文拟以江淮官话的南京、合肥、南通三种方言的单元音为例,从声学实验的角度,以性别的社会变异为重点,探索生理差异与社会变异计算方法的应用,以期对汉语元音的性别变异问题有较细致的讨论和认识。 2.材料与工具 本文材料来自笔者的田野调查,包括南京话、合肥话和南通话的单元音数据。南京话有11个单元音,分别是
多见于男性,而少见于女性(吴波2017)。由于实验语音学的介入,方言语音的描写正逐渐走向新描写主义的精细化道路。目前有关汉语方言语音的性别变异一方面多限于描写性比较,对其计量方法的探索还存有空白;另一方面由于男女声带与声腔构造的差别,元音的生理差异易于解释,但其社会变异研究仍有待进一步深入。 有鉴于此,本文在新描写主义的背景下(胡建华2018),把性别变异分出生理差异与社会变异两种类型进行分析,拟讨论的问题主要有三:1)如何量化语音的生理差异尺度;2)在社会变异分析中如何消减生理因素的影响得到社会性数据;3)如何量化社会变异及其强弱。带着这些问题,下文拟以江淮官话的南京、合肥、南通三种方言的单元音为例,从声学实验的角度,以性别的社会变异为重点,探索生理差异与社会变异计算方法的应用,以期对汉语元音的性别变异问题有较细致的讨论和认识。 2.材料与工具 本文材料来自笔者的田野调查,包括南京话、合肥话和南通话的单元音数据。南京话有11个单元音,分别是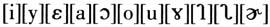 ①;合肥话共有单元音12个,分别是
①;合肥话共有单元音12个,分别是 ②;南通话共有单元音12个,分别是:
②;南通话共有单元音12个,分别是: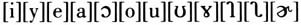 ③。南京话、南通话的发音人各有3男3女,合肥话5男5女,年龄均在20-25岁之间。数据采集时分单字音与载体库两种,调查例字为(C)V结构,具体说明如下: 1)每类元音设计例字2例,首选平调的零声母和唇音声母音节,没有的选声韵自然匹配式音节。每个例字发音5遍,每遍随机打乱。 2)载体库形式为“我来读*这个字”,“*”即对应的单字库例字,每个样本发音5遍。将三点合并在一起共得到18类单元音。前期实验发现单字与载体环境中,性别变异无显著性差异,故下文将两类数据合在一起分析,有效样本量见下表统计:
③。南京话、南通话的发音人各有3男3女,合肥话5男5女,年龄均在20-25岁之间。数据采集时分单字音与载体库两种,调查例字为(C)V结构,具体说明如下: 1)每类元音设计例字2例,首选平调的零声母和唇音声母音节,没有的选声韵自然匹配式音节。每个例字发音5遍,每遍随机打乱。 2)载体库形式为“我来读*这个字”,“*”即对应的单字库例字,每个样本发音5遍。将三点合并在一起共得到18类单元音。前期实验发现单字与载体环境中,性别变异无显著性差异,故下文将两类数据合在一起分析,有效样本量见下表统计: 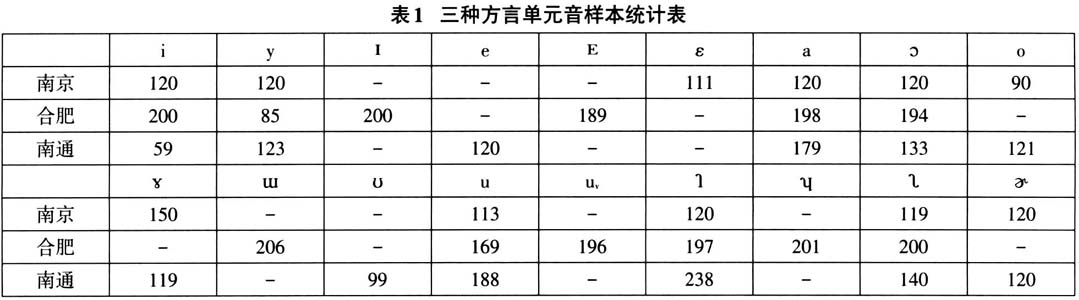 录音参数为44 100Hz,数据分析时统一转换为16 000Hz,采样精度16-bit,单声道。录音软件采用的是中国社会科学院语言所熊子瑜开发的xRecorder,数据标注软件为Emu Database Tool,由慕尼黑大学语音与言语处理所开发,共振峰等相关数据由该软件的Tkassp模块实现,数据分析函数来自R语言相关工具包④(Harrington 2010)。 3.分析与结果 3.1 生理差异的归一化系数 由于个体声道结构的差异,即使是同一个元音,由不同的说话人发出来,它的共振峰结构也一定会存在差异。在变异研究中,以初始赫兹(Hz)为尺度时,不宜直接进行比较分析,因为我们无法判定这些差异是语言学意义上的,还是个体生理结构上的,这是元音声学研究的共识。因此在多样本的统计分析中,就需要对频率(Hz)进行某种转换处理,归一化就是实现这种转换的主要方法。研究者们很早就关注了元音的性别变异问题,如Peterson和Barney(1952)对北美英语单元音的共振频率(
录音参数为44 100Hz,数据分析时统一转换为16 000Hz,采样精度16-bit,单声道。录音软件采用的是中国社会科学院语言所熊子瑜开发的xRecorder,数据标注软件为Emu Database Tool,由慕尼黑大学语音与言语处理所开发,共振峰等相关数据由该软件的Tkassp模块实现,数据分析函数来自R语言相关工具包④(Harrington 2010)。 3.分析与结果 3.1 生理差异的归一化系数 由于个体声道结构的差异,即使是同一个元音,由不同的说话人发出来,它的共振峰结构也一定会存在差异。在变异研究中,以初始赫兹(Hz)为尺度时,不宜直接进行比较分析,因为我们无法判定这些差异是语言学意义上的,还是个体生理结构上的,这是元音声学研究的共识。因此在多样本的统计分析中,就需要对频率(Hz)进行某种转换处理,归一化就是实现这种转换的主要方法。研究者们很早就关注了元音的性别变异问题,如Peterson和Barney(1952)对北美英语单元音的共振频率(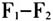 )的性别变异的分析结果是,女性比男性平均约高出20%左右;Fant(1959)对瑞典语的研究得出的参考值为17%左右。但两项研究都是基于初始的赫兹单位,未做进一步的归一化处理。
)的性别变异的分析结果是,女性比男性平均约高出20%左右;Fant(1959)对瑞典语的研究得出的参考值为17%左右。但两项研究都是基于初始的赫兹单位,未做进一步的归一化处理。 和Lindblom(1975)提出了同一归一化方法,用男女声道长度的比值作为性别差异的归一化系数k,并用这一系数对Peterson和Barney(1952)的男性、女性的元音共振峰数据进行了归一化处理,取得了良好的分析效果。他们的k值的算式如下:
和Lindblom(1975)提出了同一归一化方法,用男女声道长度的比值作为性别差异的归一化系数k,并用这一系数对Peterson和Barney(1952)的男性、女性的元音共振峰数据进行了归一化处理,取得了良好的分析效果。他们的k值的算式如下: