论台湾地区“转型正义”中的“台独”建构

      美国心理学家波斯纳提出的成长公式“经验+反思=成长”同样适用于解题能力的获得与提升.解题后的反思有利于激活数学认知，并生长相关数学思维.一方面，通过解题反思，探究解题错误的发生以及解法的发现过程，理清解题规律，理解解题关键，积累更多的解题经验；另一方面，对问题进行宏观上的进一步认识和理解，透过现象看本质，对问题进行必要的拓展和延伸，以使相关解题策略内化为个体后续解题自发的知识和能力.因此，拓展与延伸是发展数学解题思维的有效途径.一般来说，变换问题的提问方式、相关背景、形式结构和应用范围等是问题拓展与延伸的基本方略.

      一、改变问题的提问方式，变换思维模式

      对问题的拓展与延伸，首选的是改变问题的提问方式.诸如把单问改成分步设问，增加中间的设问；将结论隐蔽起来，把证明题改为探索题；等等.此外，增删已知条件、隐含条件明朗化、显性条件隐性化、直接条件间接化、抽象条件具体化和具体条件抽象化等，也都是改变问题提问方式的有效路径.

      例1 已知a，b，m都是正数，且a＜b，求证：.

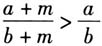      对于这道容易证明的不等式，我们可以改变提问的内容，逐步把思维引向深入.

      

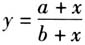      事实上，这组不等式体现了函数在区间[0，+∞）上是增函数.那么，再反过来思考：如果知道了函数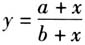的单调性，是不是也就能够证明前面的一系列不等式？由此把不等式延伸到函数，增强了数学思维的厚度.

      例2 若不等式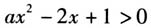对任意x∈R均成立，求实数a的取值范围.

      根据数形结合思想，容易求得a的取值范围.在此基础上，我们可以变换出下列几个逐级延伸的题目.

      

      在上述四个变式中，我们依据相关概念、公式、定理及其推理规则对原问题进行了文字语言、图形语言和符号语言之间的转换与延伸，使问题的提问方式发生了改变.虽然问题的本质并没有发生根本性变化，但是对知识与能力的考查力度显然得到了加强.

      二、革新问题的相关背景，激活思维张力

      诚如波利亚所说，货源充足和组织良好的知识库是一个解题者的重要资本，良好的组织易于用上所提供的知识，这甚至可能比知识广泛更为重要.在解题的拓展与延伸中，从不同的问题背景出发，从知识的不同模块入手，进行重组和加工，有助于巩固所学数学知识，并盘活知识覆盖面，激活思维张力.这也是实现问题拓展与延伸的又一重要路径.

      例3 已知x＞0，y＞0，2x+y=2，求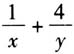的最小值.

      基于不同的视角和知识点，该题可以引申与推广如下.

      （1）在原有知识覆盖领域将条件与结论调换.

      变式1：已知x＞0，y＞0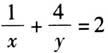，，求2x+y的最小值.

      （2）结合对数函数进行拓展.

      变式2：已知函数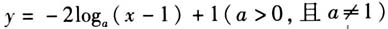的图象恒过定点A，且点A在直线mx+ny-4=0上，其中mn＞0，求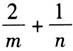的最小值.

      根据题意，可知点A的坐标为（2，1）.代入直线方程，得2m+n=4.该题转化为：若2m+n=4，且mn＞0，求的最小值.