中国古代文论的理论自觉与阐释学重构

      一、问题提出

      教材是根据课程标准编写的教学规范用书，是老师上课的主要参考材料.英国剑桥大学Ken Ruthven在2014年数学教材研究与发展国际会议中指出：当今数学教材的形式及其在数学教学中的地位发生了很大变化，对教材的研究分析应该受到人们更多的重视[1].

      作为代数与几何交界处的内容，一方面，“圆锥曲线”是高中数学中十分重要的内容，同时也是高考中占比大、难度高的部分，蕴含着数形结合、函数与方程、转化与化归等丰富的数学思想；另一方面，“圆锥曲线”与科研、生产以及人类的生活具有十分密切的联系[2].然而，通过文献分析发现很多研究是从宏观层面分析一本教材或者几何与代数等的某一模块内容，很少有研究者去研究一个特定数学内容概念化、结构化的呈现方式[3]，而关于“圆锥曲线”部分的研究就更少之又少了.通过对中美教材“圆锥曲线”部分进行比较研究，改进课程与教学，可以帮助学生掌握数学的思想方法，提高学生的学习成绩，使学生认识到圆锥曲线与其他科学的联系并将其应用到实际生活.

      本研究选取中国和美国数学教材“圆锥曲线”内容作为研究对象，从内容呈现特征、内容呈现结构、例题与习题四方面进行比较，分析两个国家数学教材的特色与差异，总结教材中关于圆锥曲线部分的设计与编排启示.

      二、研究设计

      （一）研究样本

      国内选取使用范围最广的人民教育出版社2008年出版的数学A版教材《数学必修2》和《数学选修2-1》（以下简称人教版）；美国没有全国性的教材评审机构，联邦政府教育部没有对中小学教材进行审定的责任与义务，教材的评估与选定根据各州的实际情况而定，因此选取美国使用范围很广的全球知名出版公司Pearson教育集团2008年出版的《Algebra2》（以下简称PR版）.

      （二）研究方法

      定性描述与定量刻画相结合的方法.

      三、研究结果

      （一）内容呈现特征

      1.宏观比较

      内容呈现结构的宏观方面将从内容所占页数、直观特点和栏目设置三个方面进行比较分析.

      人教版“圆锥曲线”内容所占页数多于PR版，分别为为77页和59页，且两个版本教材每页所承载的内容量大体相同.

      直观特点方面，PR版教材比人教版更加色彩艳丽、形象直观.PR版教材视觉效果华丽，将概念、定理等用不同色彩的底色衬托或者用方框标出，实物图、彩色照片的数量丰富，内容更加直观形象；人教版教材概念、定理等的标注没有PR版醒目直观，彩色图片等偏少.PR版教材视觉感受更加舒适，更加具有趣味性和感知性，但是图片繁多有可能分散学生对具体数学知识的注意力，对于抽象思维能力较高的高中生是否还要进行这样的处理需要教育学、心理学等相关研究者进行更加深入的分析研究.

      人教版和PR版“圆锥曲线”内容的栏目设置如表1.

      

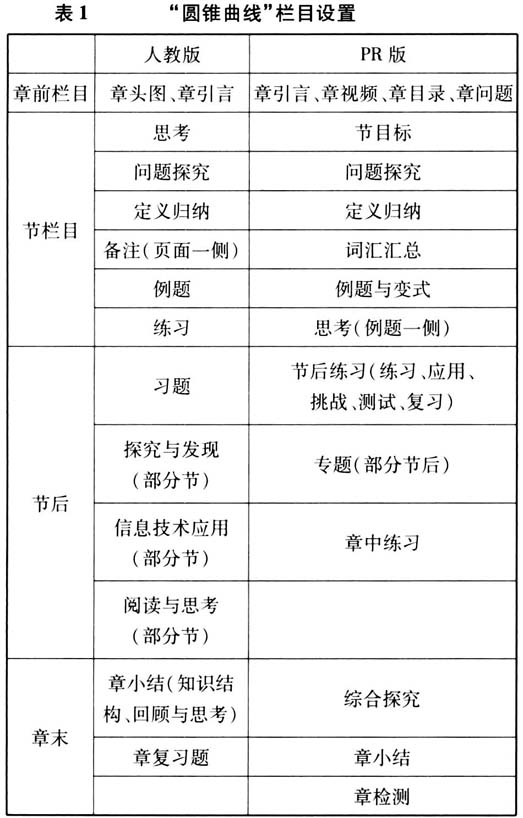      人教版和PR版“圆锥曲线”内容栏目设置都十分丰富，各有特色.人教版阅读思考等为其特色栏目，提供一些数学史故事、数学问题供学生阅读；PR版节目标、专题为其特色栏目.

      PR版教材可读性更强，有利于学生自学.PR版教材在一节内容开始之前列出该节学习目标，学生通过学习目标获得本节主要学习内容、重点内容等，从而更好地进行接下来的学习.当前高中生的抽象能力已经随年龄增长大大增强，及时引导学生进行自学有利于学生在不断解决数学问题、克服数学苦难的过程中逐渐增强学习信心，提高学生学习数学的兴趣，有利于教师有针对性地进行教学，增强学习效率[4].

      PR版教材部分章节后面会有节后专题，主要介绍一种与前节知识相关的数学思想方法或技能，如在第一节“圆锥曲线探索”之后有“用图形计算器画圆锥曲线”的专题.这样的设计安排一方面可以帮助学生巩固所学知识，另一方面，学生使用计算软件的能力在专题训练中得到加强.

      2.微观比较

      内容呈现特征的微观方面从信息技术运用和数学史融入两个方面进行比较.

      根据两版本教材信息技术使用的特点将信息技术使用方式分为解题、验证、探究、引入新知四类.解题为要求使用信息技术进行解题；验证为使用信息技术验证所得答案的正确性；探究为使用信息技术进行探究性的活动；引入新知为使用信息技术分析问题从而引入新的知识.人教版和PR版“圆锥曲线”内容信息技术使用的数量及方式如表2.

      

      首先，PR版“圆锥曲线”内容信息技术运用数量远大于人教版；其次，人教版信息技术被均匀用于解题、探究和引入新知，而PR版主要用于解题；另外，人教版注重几何画板的使用，PR版注重图形计算器的使用；特别的，PR版会有信息技术的专题，如在第一节后的专题“用图形计算器画圆锥曲线图象”培养学生使用图形计算器的能力.

      汪晓勤按照数学史与数学知识的关联程度，将数学教材运用数学史的方式分为五类：点缀式、附加式、复制式、顺应式、重构式[5].人教版“圆锥曲线”内容有两处数学史的融入，分别在章引言和阅读与思考部分，在章引言部分介绍了笛卡尔坐标系，在阅读与思考部分介绍了坐标法与机器证明的发展过程，融入数学史的方式均为附加式；PR版教材中无数学史的引用.