我国教育财政投入记忆性的实证研究

       改革开放以来，在宏观社会经济发展和教育财政投入制度改革等动力机制的驱动下，我国财政性教育经费呈现出较快的增长态势。如表1所示，1980年，我国财政性教育经费为134.89亿元，经历了30多年的增长，2016年我国财政性教育经费首次突破3万亿元，总额高达31373亿元，以1980年的价格作为不变价格，扣除物价变动因素后，2016年我国财政性教育经费实际值为5505.19亿元，比1980年增加了5370.3亿元，实际年均增幅保持在10％以上。

      

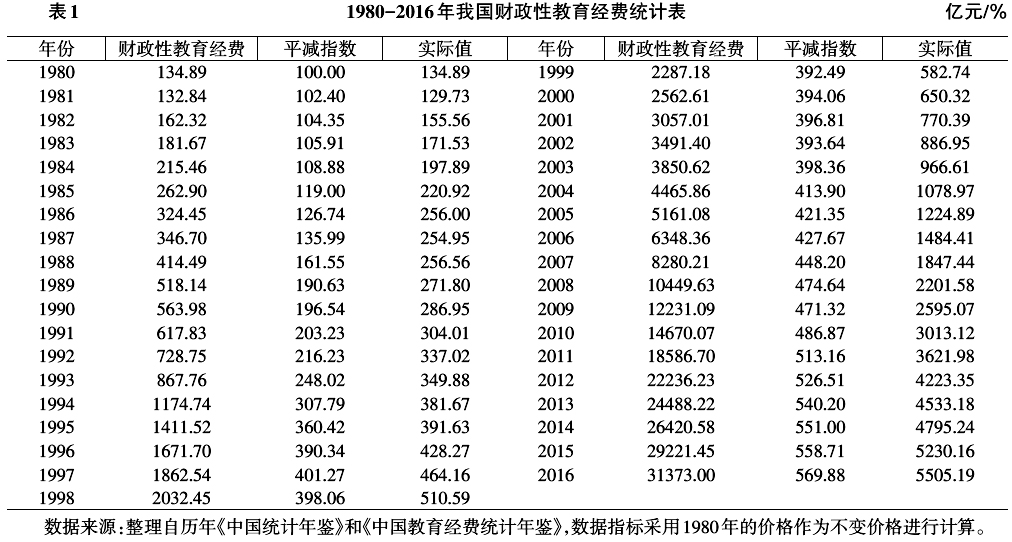       作为政府教育财政投入规模的量化指标，财政性教育经费占国内生产总值(GDP)和财政支出的比例常常被用作判断教育经费充足与否的评价标准。1993年2月，国务院审议并颁布了《中国教育改革和发展纲要》，纲要中正式确立我国教育财政投入的战略目标，决定逐步提高国家财政性教育经费支出总量，在20世纪末达到当年GDP比例的4％。2012年，我国财政性教育经费总额为22236.23亿元，占当年GDP的4.28％、财政支出的17.69％，首次达到并超过教育财政投入4％的战略目标。

       长期以来，我国教育财政投入受教育财政投入4％行政命令的影响较大，在教育财政投入制度尚不完善的情况下，这种单一的扩展或复制不可避免的会受到来自“教育资源稀缺性”和“行政命令红利枯竭”等方面的限制，导致财政性教育经费的增长缺乏长效性。通过对我国改革开放以来财政性教育经费实际增长状况的分析，可以发现在扣除物价变动因素之后，我国财政性教育经费在1981年和1987年等年份中均出现了明显的负增长情况，教育财政投入增长在当前各种机制的作用下存在着诸多的不确定性因素。

       目前，我国经济正在向形态更高级、分工更复杂、结构更合理的阶段演化，经济运行处于深度调整期及矛盾消化期，经济发展步入“新常态”。教育服务作为准公共物品，不仅具有公共物品在消费侧层面的非排他性和非竞争性，还具有供给侧层面的制度性和阶段性，以“新常态”为标志的经济社会结构转型将对教育财政投入的持续性形成巨大挑战。2012年以来，伴随着教育财政投入4％“政策红利”的释放，教育财政投入随即出现增速放缓的迹象，2016年我国财政性教育经费为31373亿元，同比增长7.36％，远低于2012年19.64％的增长速度，占GDP比重由2012年的4.28％跌至4.22％。因此，我国教育财政投入在“后4％时代”能否延续前一阶段的增长趋势，保持持续增长，成为当前亟需回答的问题。

       通常情况下，在研究价格或经费波动的自相关性和记忆性过程中，许多学者采用改进的分数布朗运动模型作为分析工具，而这类分析记忆性的过程基本可以分为高斯过程和非高斯过程两大类。其中高斯过程主要包括：分数布朗运动、子分数布朗运动(Sub-fractional Brownian motion)、混合分数布朗运动、多尺度分数布朗运动(Multiscale fractional Brownian motion)、二元分数布朗运动(Bi-fractional Brownian motion)、索引集分数布朗运动(Set-in-dexed fractional Brownian motion)和格兰蒂斯夫过程(Gladyshev processes)等；而非高斯过程包括罗布森特过程(Rosenblatt process)等。[1]由于分数布朗运动是一种高斯过程，具有加法不变性、长期相关性、厚尾性和非连续性等特征，使得分数布朗运动成为研究价格或经费波动的优良工具。[2]

       基于上述宏观社会经济和教育事业发展背景，本文将我国教育财政投入的研究问题，纳入分数布朗模型的分析框架，从而对当前我国财政性教育经费增长的记忆性进行综合判断。

       一、分数布朗运动模型的研究综述

       布朗运动(Brownian motion)最早是由英国植物学家布朗(Robert Brown,1827)提出的，他通过对花粉微粒在液体表面运动状态的观察，发现花粉微粒在液体中受到来自水分子不同方向的作用力，会呈现出无规则的运动状态。随后，美国数学家诺伯特·维纳(Norbert Wiener,1918)对这一现象做出了严密的数学分析，提出了布朗运动的积分方程和定义测度，为其在随机微分方程的研究领域奠定了基础性地位。[3]

       (一)分数布朗运动模型的概述

       1941年，苏联数学家柯尔莫哥洛夫(Kolmogorov)基于希尔伯特空间(Hilbert space)理论，进一步分析和定义了分数布朗运动，并给出了基于标准布朗运动的随机积分表达式。在此之后，英国水文专家赫斯特(Hurst,1951)在研究尼罗河水库的长期储存能力时，发现运用分数布朗运动方法能够更为贴切的表述实际状况，与此同时他设定了赫斯特指数(Hurst exponent)，并将该指数作为判断时间序列数据是否服从分数布朗运动的一个重要指标。一般情况下，赫斯特指数H取值在0到1之间，不同的取值表达出不同的实际状况。20世纪90年代末，美国数学家本华·曼德博(Benoit Mandelbrot,1997)和苏联数学家Shiryaev A N(1999)分别指出：推动价格变动的随机噪声不应该是布朗运动，而应该是分数布朗运动。其中赫斯特指数H≠1/2。