知道吗？在实际生活工作中，自然数1～9的出现概率并不是相同，除数字1始终占据约三分之一的出现频率外，数字2的出现频率为17.6%，3出现的频率为12.5%，依次递减，9的出现频率是4.6%。1938年，物理学家法兰克·本福特发现了这一现象，并通过数据验证了它。Benford法则，即F（d）=log[1+（1/d）]，此公式中F代表频率，D代表待求证数字。利用Benford法则进行审计分析对于数量多、个体数值较为平均的审计数据样本，是一个较好的补充。 近期常州市审计局在实施的审计项目中通过ASL语言和自动审计模块，将Benford法则分析功能集成至AO现场审计实施系统，以人机交互和图表展现的方式简化Benford法则分析功能的实现，降低审计人员实施Benford法则分析的门槛，使得审计人员能更直观、便捷、高效地进行该项审计活动。 一、Benford法则应用于审计疑点发现的现实意义 传统的审计分析方法在使用中过滤了大量的详细交易信息，而这些信息常常隐含了舞弊活动。Benford法则是数据式审计模式下，基于详细交易数据的分析性复核方法，这种方法通过分析数据的统计规律发现异常，从而定位异常，以便后续审计查证工作。Benford法则对审计人员的审计专业经验和专业判断依赖程度不高，非常适合普通审计人员使用。运用Benford法则进行分析和检测，可以提高审计数据的质量，使有效审查数据量大大缩小，提高审计工作效率，在一定程度上降低审计风险。 二、数据准备 以“某事业单位财务账套凭证表（base）”为例，对表中“借”字段进行分析。需事先准备“标准概率表（sheet）”作为Benford法则分析过程的参照标准。“标准概率表（sheet）”是根据美国国家标准和技术学院（NIST）给出的Benford法则定义“对于许多种类的统计数据，其首位数字是数字d的概率为lg（1+1/d），d=（1，2，3，..9）”，事先计算出的1至9999在自然界中的数字分布频率，其中（a）字段是1至9999的数值，（b）字段是数值对应的分布频率。 三、实施步骤 （一）对被审计数据进行分析，初步判断该数据是否符合Benford法则的分析条件，选择待分析的目标字段。 （二）编写审计方法，对被审计数据进行整理，形成审计分析中间表。该步骤，需对本方法涉及的测试数据“某事业单位财务账套凭证表（base）”的“借”字段去0，去NULL值，为便于后续步骤取数值位，将“借”字段所有财务发生额数据乘以100，去除小数点。本步骤涉及的ASL语句如下： sqlt； begin ExecuteUpdate（'ALTER TABLE base add COLUMN IdCOUNTER（1，1）'）； executeupdate（'alter table base alter columnidinteger'）； createtemptable（'tmp'，'SELECTbase.ID，abs（base.借）*100ASj FROM base WHERE（（Not（base.借）Is Null And（base.借）＜＞0））'）； createtemptable（'yd'，'select top1 *from tmp'）； createtemptable（'blt'，'select top 1 id as num，j asbl from tmp'）； executeupdate（'alter table blt add column bz double'）； executeupdate（'alter table blt add column bfb double'）；end. （三）对测试数据进行首位有效数字Benford法则的符合性测试，根据输出柱状图，初步发现测试线索和重点，并可根据需要，将计算比率与标准比率的差异率输出至“未落实疑点”。该步骤具体操作和示例如下： 1.执行方法后，弹出输入框，如下图所示，第一阶段先对首位数值1～9进行符合性测试，这边输入占位符“_”。
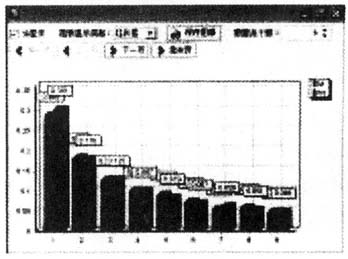
2.输入“_”后，点击“确定”后，输出首位数值1～9的计算概率与标准概率对比柱状图，如下图所示，通过观察，可以看出首位数字为“1、5、7”的数据与标准标准概率差异较大。同时，审计人员也可根据自身习惯，将图表显示类型调整为：线性图、饼图和散列图。
3.关闭柱状图显示后，弹出输入框，如下图，审计人员根据实际情况，选择是否输出1～9的计算概率与标准概率的差异率表至“未落实疑点”。
