[中图分类号]F821.5 [文献标识码]A [文章编号]1000-114X(2016)06-0084-06 澳门自回归以来,消费物价指数(CPI)走势呈现出两个明显不同的阶段。前期(2000年1月~2004年5月)CPI为负增长,通胀率均在零以下,表现为通货紧缩,这主要是受1997年亚洲金融危机的影响,经济增速放缓及社会需求收缩,促使物价下滑。后一阶段(2004年6月至今)随着澳门赌权和大陆游客自由行的相继开放,在旅游博彩业的带动下,经济高速增长,相应地CPI由负转正后经历了三个通货膨胀周期。先是于2006年5月达到6.33的高位,在略有回落后再次于2008年3月冲高至9.49,随后的2009年CPI快速下降,一度跌至2009年10月的-1.1,然后重新掉头向上攀升,于2011年12月再次达到6.81,至今仍在高位徘徊①。 通货膨胀给社会造成一定程度的损失基本上已成为共识。由此而引申出对这种损失进行度量,以力求能清晰地观察不同的通胀程度会对社会带来多大的损失。Sidrauski(1967)认为物价上涨必然令全社会的实际货币余额下降,从而对社会各部门及个体造成福利损失,即形成社会福利成本。由此提出了通货膨胀社会福利成本的定义,即:面对通货膨胀,经济部门和个体被迫改变持有货币的经济行为所造成的效率损失②。 Bailey(1956)最早展开了对通货膨胀社会福利成本的估算,利用消费者剩余对价格变化所带来的福利水平变化进行测量,该方法被称为消费者剩余法,是通过计算名义利率下降时货币需求逆函数下的面积,并指出该面积就是因通货膨胀而造成的福利损失部分③。Sidrauski(1967)构建起货币效用模型(Money in Utility,MIU),其方法是在无限期生存的典型代理人模型和Solow-Swan模型中分别导入实际货币余额并进行推导而成,货币效用模型为度量通货膨胀社会福利成本提供了一个一般均衡的理论基础④。Cooley和Hansen(1989、1991)认为货币的持有受现金的约束,并将商品分为现金商品和信用商品2类,前者是指受现金约束的一般消费品,后者是指闲暇和投资,并进一步假设个人效用是消费与闲暇共同的函数,而通胀水平会影响个人的消费决策,因此通胀率水平的高低会形成不同的稳态消费,据此可对通胀的福利成本进行估算,此理论发展而成的模型被称为现金优先模型(Cash in Advance,CIA)⑤。Lucas(2000)根据上述多个理论模型,以个体效用优化为出发点,构建起通货膨胀社会福利成本的具体测算模型,并估计了1900-1994年美国因通胀所产生的社会福利成本⑥。 上述三种模型在估算通货膨胀的福利成本中被较为广泛采用,此外国外学者还提出了时间购物模型(Brock,1974;McCallum and Goodfriend,1987)、不完全市场模型(Imrohoroglu,1992)、家庭异质性模型(Erosa and Ventura,2002)、货币搜寻模型(Lagos and Wriht,2005),以及新凯恩斯主义宏观经济学模型(Woodford,2001;Razin and Yuen,2002)等多种模型,从不同的角度分析并估算通货膨胀的福利成本。陈彦斌、马莉莉(2007)和谭硕等(2008)对国际上的相关研究进行了较为详细的综述⑦;在我国有关通货膨胀福利成本研究的论文中,大都对国内运用不同的模型作实证估算进行了简要的评述,在此不再赘述。澳门作为一个微型经济体,近年的通货膨胀较为严峻,而对通胀福利成本的研究却仍阙如,本文将在这方面作些探讨。我们采用传统的消费者剩余方法,并根据Lucas(2000)双对数函数的改进,测算澳门通货膨胀的社会福利成本率,估计通胀水平带来的社会福利损失数额,以及占经济总量的大致比例,并将这一损失与美国和中国内地的相关研究进行比较,以帮助观察澳门通货膨胀社会福利损失的程度。 二、模型、变量及数据处理 在现实经济当中,若名义利率大于零,通胀率便超过最优通胀水平,货币的配置处于非均衡状态,社会整体福利下降,因此而要付出福利成本。Bailey(1956)设定,当名义利率从0上升至i时,逆货币需求函数下方的面积就是通货膨胀的福利成本。

Bailey采用半对数货币需求函数衡量通货膨胀的福利成本,即:
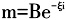
。而Lucas(2000)认为采用半对数货币需求函数模型对高通胀或名义利率接近0时的货币需求进行估算,拟合的效果会比较好;若在中性通货膨胀时,双对数货币需求函数会有比较好的拟合效果,即:
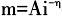
(Lucas,2000)。将双对数函数引入(1)式得:
 Bailey采用半对数货币需求函数衡量通货膨胀的福利成本,即:
Bailey采用半对数货币需求函数衡量通货膨胀的福利成本,即: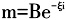 。而Lucas(2000)认为采用半对数货币需求函数模型对高通胀或名义利率接近0时的货币需求进行估算,拟合的效果会比较好;若在中性通货膨胀时,双对数货币需求函数会有比较好的拟合效果,即:
。而Lucas(2000)认为采用半对数货币需求函数模型对高通胀或名义利率接近0时的货币需求进行估算,拟合的效果会比较好;若在中性通货膨胀时,双对数货币需求函数会有比较好的拟合效果,即: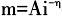 (Lucas,2000)。将双对数函数引入(1)式得:
(Lucas,2000)。将双对数函数引入(1)式得: