整体与直觉　　

      作为物理学家的海森伯(Werner Karl Heisenberg，又译“海森堡”)被公认为20世纪的科学巨擘，其所提出的测不准原理堪与爱因斯坦的相对论比肩。主要是由于这一原理的提出，他荣获1932年的诺贝尔物理学奖。海森伯作为哲学家的地位也牢不可破，其关于主体性的科学论证和强调成为哲学系学生的必备知识。兴起于19世纪60年代的后现代主义思潮经常被溯源到他的测不准原理。(cf.Hassen，pp.55-63)然以其科学研究(量子力学和粒子统一场论)为基础，作为其哲学组成部分的美学论述则相对说来乏人探问。不过，这冷落并不意味着没有价值，而是说人们尚未认识到其价值。

      鉴于此，笔者在此文中力求客观“认识”海森伯的科学美学思想，并在它与当代语境之间建立某种“价值”关系。二者并不分裂，“认识”中包含着“价值”，而“价值”也是一种“认识”。古语“管窥”(或“蠡测”)即此之谓也：它不只表达谦逊的美德，更道出一个事实，即任何认识都实在地处于某种情境之中。此情境，海森伯更愿意理解为科学实验的工具或条件。

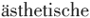      海森伯试图在科学与艺术或美学之间寻找或建构共通点。例如在其传记性著作《部分与整体》的序言部分，他希望通过返回“科学是由人所从事的”这一不证自明的事实，以“缩小在精神科学—艺术与技术—自然科学两种文化之间那经常令人哀叹的鸿沟”。(Heisenberg，1979，S.7)该书记载，在一次与爱因斯坦的谈话中，他坚持认为数学形式既代表了自然界的真正特征，也隐含着我们与自然界的思维关系；它们既是单纯的，也是美丽的。在谈到“数学形式”(mathematische Formen)或“图式”(Schema)之单纯和美丽时，海森伯情不自禁地启动了“美学的真理标准”(ein Wahrheitskriterium)。(cf.ibid，S.85-86)这也就是说，他在数学形式中发现了美；简言之，数学形式在他看来就是美。

      在《越界》一书中，海森伯更是系统地在“精密科学中”发掘“美的意义”。海森伯的《越界》一书收录了其一篇名为《精密科学中美的意义》(“The meaning of beauty in the exact sciences”)的讲演(1970年)。该文可视为海森伯的美学代表作。针对那种以为“自然科学和技术只是盯着准确的观察以及理性和分析的思想”的观点，他反驳：“不错，这种理性的思维和精心的测量属于科学家的工作，就像锤子和凿子属于雕刻家的工作一样。但是，在两种情况下，它们都只是工作的工具，而非工作的内容。”(Heisenberg，1974，p.182)海森伯将科学家与艺术家的区别降低到工具层面，而在内容层面，在本质上，他们实则做着一样的事情。这个事情在他对开普勒一则拉丁语格言的翻译和改写中透露了出来。开普勒的格言是“Geometria est archetypus pulchritudinis mundi”。他将其中的“几何”替换为“数学”，翻译为：“数学乃世界之美的原型。”(Heisenberg，1974，p.182)或许如果依其本心，“数学”也是可以替换为“科学”的。通过这一格言，再或者假定可以被继续扩大的，海森伯意欲表达的是：第一，科学的事业就是美的事业；第二，反过来说，艺术的美的事业也是科学的事业；第三，科学与艺术之共同的事业，即美的事业，乃是对原型的揭示。

      何谓“原型”？它有怎样的特点？用科学的术语说，这“原型”是海森伯在其统一场论中所苦苦追寻的“数学形式”；从哲学史上说，是毕达哥拉斯的“数”和柏拉图的“理式”(Idea，多译为“理念”)；从一般的思维规律看，是“抽象”和“统一”，是事物之间或其浮表下隐秘的“连结”。海森伯指出：“理解意味着认出连结，意味着把个体看作某种更普遍之物的一个殊例。但是走向更大的普遍性本身即总是走向抽象——或者更准确地说，走向下一个最高层次的抽象；因为，那更高级别的普遍在一个统一的视点下整合了许许多多各不相同的个别事物或过程，这意味着它同时也舍弃了那些被认为是无足轻重的特点。换言之，它从它们中抽象出来。”(ibid，p.144)在另一处，海森伯说过类似的话：“理解一向不过就是对于连结的感知，也就是说，从多样性中感知到整体性特征或者相似性印迹。”(ibid，p.168)但是，海森伯并不把对“连结”或“原型”的理解和把握看作普通的认识活动；毋宁说，他是反过来把一切认识活动都视之为美学活动：

      假定说美被构想为部分与部分之间以及部分对整体的协调，再假定说，另一方面，所有理解都首先是由这一形式上的连结而造成的，那么对美的体验实质上就无异于对连结的体验，无论是被理解到的连结抑或至少是被猜测到的连结。(ibid，p.170)

      以对“形式”或“连结”的领会和体验，海森伯建立起“智与美”之间、数学或科学与艺术或美学之间的往来交通以至于相互置换。分开来说，对“形式”或“连结”的领会和体验既是审美活动的本质特征，也是科学活动的本质特征。海森伯接受了古代思想家关于美的两个定义：一是视美为部分与部分之间以及部分对整体的恰到好处的协调，二是将美作为“一”之永恒光辉穿过冥顽拙滞的物质现象的熹微。虽然在历史上曾经争锋相对、互不相让，但是海森伯认为：“事实上两种定义并非相距甚远。”(ibid，p.183)海森伯没有明言何以二者相距弗远，但他的意思在字里行间还是离离可辨的：前一定义中的“整体”即是后一定义中的“一”，它们都是相对于繁茂芜杂的现象界而言的，是对各种现象的统合和抽象，或者说是各种现象的“原型”，而现象或“杂多”则是它们的复制品。

      海森伯将这两个美的定义或者说将“原型”“连结”“整体”“一”诸概念与毕达哥拉斯的“数”和柏拉图的“理式”联系起来。这样做对于海森伯的美学具有决定性的意义。这当然不只是说，他借毕达哥拉斯和柏拉图之力——在他看来，两位前贤既是科学的先驱，也是美学的先驱(cf.ibid，p.172)——轻松打通了其统一场论或广义而言科学与美学或艺术的联系。毕达哥拉斯关于数学与音乐关系的论述已经帮助他很好地完成了这一任务。他之进一步引入柏拉图的“理式”除了强化他从毕达哥拉斯那里得到的启示即“理式”如“数”一样也是美本身或美的源泉之外，还将对于“理式”和“美”的认识方式作为一个重大的问题提了出来。他认为柏拉图的《斐德罗篇》(251ff)表达了如下思想：“一旦见到美，灵魂便惊惧不已，身体发颤，因为它感觉到有某种东西从它身上被召唤出来，这种东西不是感官从外部所给予它的，而总是已经被放置在那里，在其中一个幽深的无意识区域。”(Heisenberg，1974，p.171)既然柏拉图“美”的“理式”藏身于“无意识”区域，那么我们就无法循着“意识”之径来达到它了。海森伯断言：“人类心灵对于理式的把握与其说是知解力所传达的一种知识，毋宁说是一种艺术直觉，一种半意识的朦胧感知。”(Heisenberg，1974，p.171)