动态与资讯

      课堂是落实核心素养的主道，作业是培育核心素养的辅道.在数学教与学中，由于应试思想使然，教师往往对“提分性”书面作业重视有余，对创造性、实践性作业思考不足；学生因繁难的“题海”学业负担变重、数学兴趣索然，数学素养的培养也因此受到影响.《普通高中数学课程标准（2017年版）》（以下简称课标）在教学建议中指出：“要树立以发展学生数学核心素养为导向的教学意识，将数学核心素养的培养贯穿于教学活动的全过程.教师要善于根据不同的内容和学习任务采用不同的教学方式，抓住关键的教学与学习环节，增强实效.”

      一、单元小结时，指导学生自编试题

      学生自编习题的过程，就是对所学知识不断强化与训练的过程.在这个过程中，从简单到复杂、从模仿到创新，学生对数学概念、公式、定理、法则的理解会更加深入，对知识的应用会更加灵活，对题型、题目的组成结构会更加了解，分析问题和解决问题的能力会得到进一步发展.自编试题为培养逻辑思维能力和创新能力搭建了一个良好平台，为学生打开了一扇主动学习数学的“智慧之窗”.由于缺乏命题经验和知识储备，学生自编试题在科学性、准确性、规范性上可能出现瑕疵，但不影响学生主动获得知识、培养能力和发展数学素养.

      学完一个单元知识，学生对该内容有了全面、系统性的认识，对本节知识的重点、难点更敏感.这时让学生进行自编试题训练，利于构建知识网络和锻炼综合运用知识的能力，使学生在“知识理解、知识迁移、知识创新”数学核心素养的三级水平上都能得到不同程度的发展.

      案例1 均值不等式的运用

      学完人教A版《数学必修5》“基本不等式”单元后，在小结复习中，笔者请同学以学过的知识为载体，模仿做过的习题，编制考查“均值不等式运用”的试题.

      

      （4）一天，N先生送了100颗向日葵种子给M小姐作生日礼物.M小姐将向日葵种子围成一个等腰三角形，每粒种子间隔1个单位长度，设该三角形的面积为S，若S      

      学生大都采用“倒推构造，调整数据”的设计思路编制试题.即先考虑好要考查的要点和方法，再构造一个能用均值不等式的式子，然后调整数据设置能得到该式子的条件.学生觉得在编题中最难的是配置合理、好算的已知数据.从立意到雏题，再到成题，是学生对领会考查意图、明确考查知识、选用解题方法、厘清知识交汇的“一条龙式”自我训练，是一次自发性地元认知监控能力的检测提升过程.例如原创题（1），命题者想在“和、积转换运算”中考查运用均值不等式求最值，于是构造了等式mn=m+n+3，然后用逆向思维，演绎倒推能得出该等式的条件.为了体现知识的交汇性、综合性，学生绞尽脑汁、几经调适，最终将直线斜率、指数函数性质、三角函数运算、均值不等式融为一体.再如自编错题中，学生自我发现、自我矫正了正弦定理的推理错误.

      为了编制一道有质量的试题，学生经历了细致深入地有逻辑地思考问题的过程，历练了合乎逻辑的思维品质和理性精神.作为命题者，要分析他人对自编试题的解答情况，首先自己要能理解蕴含其中的运算对象、掌握运算法则、探究运算思路、求得运算结果，逻辑推理和数学运算素养在编题中“随风潜入夜，润物细无声”.

      二、模块拓展时，做好实习作业

      数学实习作业突出实践性、探索性，学生必须主动观察记录现象，动手操作实验，整理分析数据，经历数学建模、对比研究、逻辑推理等思维过程，依靠团队合作，才能完成任务.其过程充满乐趣与挑战，是寓学于乐的开放性数学活动，也是培育数学核心素养的一个良好教学载体.高中数学教材多处设计了实习作业，但实际教学中，常常被当作非考试内容掠过，作用甚微.

      案例2 探究“冷却函数模型”

      探究“冷却函数模型”是高中数学《必修1》（人教A版）第三章“函数的应用”中的实习作业.请学生进行模拟实验，再设计方案，验证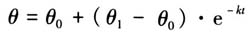这一冷却模型.看似不可能完成的任务，实际操作中学生的积极性与创造性出乎意料.

      [分组实验]用具：大、小烧杯，电炉.用电炉将大烧杯中的水加热至100C，再将初温30C的水加入小烧杯.将小烧杯置于大烧杯中水浴.每半分钟记录一次水温，持续记录5分钟.随后每一分钟记录一次水温，再持续5分钟.然后将水改为酒精再做同样实验.重复实验若干次，直到收集到几百组实验数据.为了判断实验的准确性与科学性，学生还到附近高校实验室请大学老师帮忙分析数据.

      学生学习使用Origin软件，拟合分析了33个函数，发现有多个函数图象符合预想情况.根据已有研究，确定系数R^2的值达到0.98就可以认为这是有效函数图象.故选取R^2=0.99的函数分析研究：

      

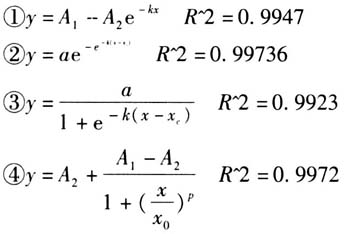      由①拟合得到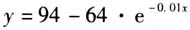，发现其最吻合实测数据.物理学家牛顿提出，当初始温度为30℃、环境温度为的100℃时，有冷却模型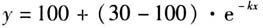：.函数①与之很相似.于是推定这组实验数据满足牛顿提出的“理想模型”.但是，学生在实验中发现k的值会随着初始温度、大气压强等因素的变化而变化.所以“理想模型”仍有优化的可能，并非完美无缺.