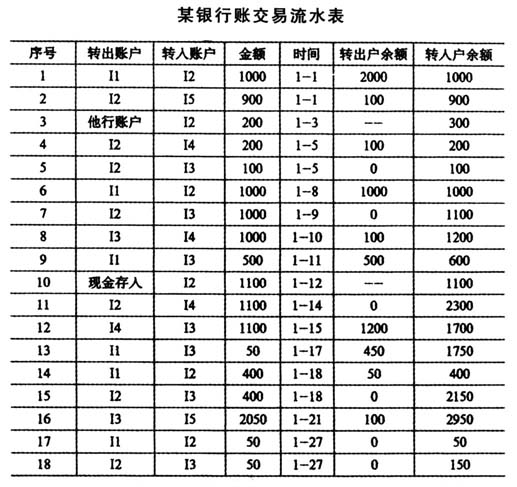
作为金融活动的载体，资金及其流动情况始终是金融审计的核心内容。审计中，常发现大量资金向个别账户聚集或在某些账户间循环的现象，与正常生产经营产生的资金流向不符，称之为异常资金流动。从近年审计情况看，异常资金流动动辄涉及数百亿元资金，是地下钱庄、集资诈骗等违法活动的重要特征。因此，准确、高效地发现异常资金流动，对于打击经济犯罪、维护市场秩序具有重要意义。 现行的审计方法及不足 在审计领域，《商业银行审计指南》针对异常资金流动设计的方法是：一是检索对公存款账户大额取现的记录，对全年单笔取现和汇总取现前十位的账户进行详细审查；二是检索单笔存取款超过一定金额的记录或将全年的发生额汇总后，审查前十位的账户。这些方法都将大额资金作为异常资金流动的唯一标志，不仅无法识别“化整为零”的流动形式，而且因为农产品收购、金融产品交易等正常经济活动也会出现大额提现或巨额资金调度的情况，“挑大户”的审计方法在一定程度上会产生误导，实际应用效果不佳。 在金融监管领域，有关专家对异常资金流动问题提出基于正常模板、扫描统计、序列匹配等离散数学原理的分析方法，其共性在于长期观察各类经济活动的资金转移过程，通过分析正常的行为习惯发现异常现象。由于审计对象差异较大，现场能够利用的数据资源和时间有限，这些方法目前多处于理论研究阶段，效果有待检验，将其直接应用于审计面临较大困难。 解决问题的思路和方法 审计人员对异常资金流动问题分析发现，大部分涉案资金均流经几个关联账户，或在由若干关联账户组成的网络中分拆、汇聚，从而达到变更资金性质、逃避额度监管、隐匿来源去向的目的。因此，在现有审计方法的基础上，增加对账户关联性的分析，有助于提高对异常资金流动的识别能力。具体需要解决两个问题：一是由账户交易流水生成完整的资金转移路径；二是从大量资金转移路径中找出频繁出现的账户集合。 （一）生成资金转移路径 由银行账户交易流水生成资金转移路径的关键在于，当B账户从A账户收到一笔资金，又向C账户转出另一笔资金，需判断C账户收到的资金是否来源于A账户。否则，则上述资金转移是两条彼此独立的路径，即（A，B）和（B，C）；反之，则应将两条路径归并为（A，B，C）。根据集合理论及审计经验，可按以下原则进行判断：假设B账户原有资金余额为B1，从A账户收到资金金额G1至转出资金给C账户期间，其他账户转入B账户的资金总和（稀释资金）为G2，B账户转给C账户的金额为P1。 若初始资金B1与稀释资金G2之和不能满足转给C账户金额P1（即B1+G2＜P1），则B账户转给C账户的资金中必然包含来自A账户的资金。上述B1、P1在银行账户交易流水中均有记录，G2能够用SQL语句统计得出。 以某银行账户交易流水为例（见下表），通过判定和记录，可生成以下九条资金转移路径： （I1，I2，I5）、（I2，I4）、（I2，I3）、（II，I2，I3，I4）、（I1，I3）、（I2，I3，I4）、（I1，I3）、（I1，I2，I3，I5）、（I1，I2，I3） （二）数据挖掘和频繁项集搜索 从运算生成的数以万计资金转移路径中找到频繁出现的账户集合，从而确定其关联性，是发现异常资金流动的重点和难点。由于子集数量随账户个数的增加呈指数增长（n个账户有2n个子集），当账户总体数量较多时难以统计所有子集的出现频率，好在数据挖掘的重要支撑——频繁项集搜索技术提供了新的思路。 项集是指项的集合，包含k个项的集合称为k项集，如资金转移路径（I2，I4）即一个2项集。项集的出现频率是包含项集的事务数，在前述例子中，事务总数为9，而项集（I2，I4）在（I2，I4）、（I2，I3，I4）和（I1，I2，I3，I4）3个事务中均出现过，因此其出现频率为3。频繁项集是指项集的出现频率大于或等于预设支持度与事务总数乘积的项集。由此可见，从众多资金转移路径中找到频繁出现的账户集合就是频繁项集搜索。 （三）Apriori算法简介 Apriori算法是最有影响的频繁项集搜索算法，目前已在网络安全监控领域获得广泛应用，其基本原理是频繁项集的所有非空子集都是频繁的。该算法使用逐层搜索的迭代方法，已发现的k项集被用于搜索k+1项集，直到能够满足频繁条件的最大项集。在前述例子中，最大项集是存在关联关系的最大账户集合。
Apriori算法由连接和剪枝两个步骤组成，在连接步骤，用频繁k项集进行自连接，形成k+1项集。在剪枝步骤，删除k+1项集中包含非频繁k项集的子集。由于进行了剪枝，该算法的复杂度仅随k指数增长而不随全部项数指数增长，因此是可控的。 （四）搜索关联账户集合 仍以前述九条资金转移路径为例，若以共同出现超过三次作为存在关联关系的判定条件，Apriori算法处理过程如下：
