论构式压制的转喻阐释

      一、引言

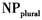      “压制”（coercion）是源于计算语言学（Pustejovsky,1991）的一个术语，泛指语言形式和所表达的语义功能之间的一种不匹配现象，如John has apple on his shirt.Give me a coffee.apple通常是可数名词，表达一个有边界的实体（Langacker,1987），但却没有出现在have a／an N或have 构式中，而是出现在have 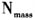构式中，apple的词义被压制成苹果碎末这样的不可数词义。coffee的情况正相反，原本是不可数实体，由于出现在可数名词构式a／an N中，词义受构式意义的压制而成为一杯咖啡这样的可数表达。近几年来，“压制”成了语言学领域中的一个新术语，随着构式语法的兴起得到了更广泛的关注（Michaelis,2004,2005；沈家煊，2006；刘宇红，2007）。本文采用Michaelis（2004）对压制的定义，即当构式的形态句法框架和填充到其中的词条语义发生冲突时，对二者所进行的协调，通常都是词条语义通过转换来满足句法框架的制约。这个定义兼顾了常规和非常规语法形式下人们对语言的创造性使用，包括对原有词汇或语句意义进行扭曲、转喻、重组和戏仿等。这些各种形式的语言活用常常互相渗透，难以严格划分，本研究主张将这些语言现象统称为压制（或糅合）（沈家煊，2006）。本文将在分析当前主要的压制研究观点基础上，将它们整合起来，建立一个广义转喻框架（GMF），以便能够对语言压制现象进行多层次、多侧面的综合描述和阐释。

      二、Jackendoff的概念结构理论对压制现象的阐释

      （1）a.Harry bent the rock.

      b.I began the book.

      c.a beer

      d.Jason smokes.

      e.Jason somked for two hours.

      岩石是宁折不弯的，（1）a有些不合常规，但人们通常可以接受这个句子，条件是需要附加上岩石具有一定柔软度的语义。（1）b也不是一个常规表达，动词began通常选择事件作为补足语，而不是一个物体，该句只能理解为began reading／writing the book。 Michaelis（2000）认为，压制现象（coercion）可以分为两种类型：向心结构的（endocentric）和离心结构的（exoeentric）。前者源于违反中心词的限制条件，如（1）a和b。后者源于由非中心词代替中心词从语义上对结构中形成姊妹关系的成分进行限制。例如，1（d）中的smokes说明Jason经常吸烟的属性，是常规用法，而1（e）中的时间状语使得smoke成为具体动作，从而产生体压制。根据句法的DP理论（Adger,2003），有些学者会认为（1）c中的a beet也是向心结构的压制现象，a为中心语，强制选择了（不可数的）单数名词beer。但根据构式语法，这是一个离心结构的压制现象，因为对于beer的重新阐释来自于整个不定冠词短语构式的压制。

      压制现象通常涉及增添句法结构所反映的意义之外的语义内容，因此，将句法、语义及语音部分作为不同系统分开处理的模块式语法理论似乎更加有解释力（Jackendoff,1997; de swart,1998）。和Chomsky一样，Jackendoff的模块语法理论也是将核心句法（core syntax）看作是自主的，不受语义等的影响，但同时将语言的语义及音系部分看作是与句法并行的模块，而不支持Chomsky句法中心主义的主张。Jackendoff的模块理论将压制现象解释为特殊语义函项的插入，这可以看作是构式内部句法—语义之间的一种糅合（沈家煊，2006）。

      Chomsky只研究句法—语义一一对应的核心句法，因此无法解释压制或糅合现象。我们可以用F（X）表示简式语义构成，即句法和语义是完全透明的对应关系，其中F代表句法中心语，X是句子补足语所表达的论元。然而，以（1）c为例，X（beer）不能看作是F（a）的适当论元，在语义构成中插入了压制函数／算子G（bottle／glass of），从而形成F（G（X））这样的语义结构，其中X是G的适当论元，而G（X）是F的适当论元（Jackendoff,1997:53）。而在。having rabbit for dinner中，X是rabbit，G是某种万能绞磨机（universal grinder），可以将X所表示的动植物可数名词变成碎末状不可数名词，F是having，以不可数名词作宾语。

      除了名词可数与不可数的转换外，Jackendoff（1997）还讨论了另一种压制现象，即指称转移（reference transfer）。（2）中原本指称食物的词the ham omelet，“包子”、“肥肠”现在转指点这些食物的顾客。

      （2）a.rhe ham omelet wants his bill.

      b.包子往里走，肥肠上二楼。

      c.三号桌还没埋单。

      Jackendoff试图说明这类现象事实上可以解释为在语义层面上将NP的简式所指X（火腿煎蛋卷、包子等）加上压制函数／算子（THE PERSON WHO ORDERED X），从而形成富式意义G（X），这样可以保持句法的自主性。他强调，能够正确运用这些富式构成的说话者对该语言要有很深的了解。人们的语言知识应该包括一个富式构成的原则，光有狭义句法决定的简式构成是不够的。以上分析也适用于（2）c，只是压制函数G有所不同。