云南省图书馆机构用户,欢迎您!
本文通过引入理性意义和内涵意义的分界,说明同语式中的同型同音成分的意义并不相同。在“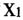 (Y)是
(Y)是 ”的格式当中,
”的格式当中,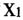 仅具有理性意义,这种理性意义即真值条件;而
仅具有理性意义,这种理性意义即真值条件;而 具有内涵意义,即社会大众或个人对X的一种普遍或主观认识,通过“是”字的判断作用,将
具有内涵意义,即社会大众或个人对X的一种普遍或主观认识,通过“是”字的判断作用,将 所具有的内涵意义赋予
所具有的内涵意义赋予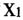 。对于这种分析,本文进行了一定的测试和证明,并对同语式的各种变体进行了说明和分析,认为不需要从构式角度进行研究,而通过格式中各个成分意义的组合就足以解析同语式。
。对于这种分析,本文进行了一定的测试和证明,并对同语式的各种变体进行了说明和分析,认为不需要从构式角度进行研究,而通过格式中各个成分意义的组合就足以解析同语式。
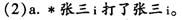
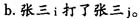 如果例(2a)中前后两个“张三”指的是同一个人,那么这个句子是不成立的,正确的说法应该是“张三打了自己”。例(2a)要想成立,前后两个“张三”必须不同指,如例(2b)所示。 那么,例(1a)-(1d)是不是违反了约束理论呢?以例(1b)为例,前一分句中的两个“科比”分明有同指关系,又显然在一个约束域内。例(1b)这种同语式在生活中并不少见,这显然给约束理论出了一道难题,难道约束域要被重新定义? 1.3 同语式与重言 “同语式”在语义学上还有另外一个名称,即“重言句”。重言(tautology)是逻辑学上的概念,宽泛地讲,是指任何情况下都成立的某些表述。用命题逻辑的术语来说,如果某一命题P永远都为真命题,那么这个恒真命题P就是重言式,所以重言式也被称为永真式。例如: (3)a.现任美国总统是奥巴马,或者不是奥巴马。 b.一加一等于二。 假设例(3a)整个句子为命题P,前一分句为命题Q,那么例(3a)可以被表述为“Q∨-Q”,在析取关系中,无论Q取真值还是假值,整个命题P的值都为真。 不过,对于重言还有另外一种狭义的理解,指的是简单的同义反复,也叫赘言,也就是相同的词语在判断句中反复出现。例如徐烈炯(1995:13)举出这样的例子: (4)启明星就是启明星。 例(4)根本不含有新的信息,在语义上形成了一个悖论。我们把例(4)这种同义反复的句子看成是狭义的重言式。按道理说,一个句子应该包含新的信息,否则就是废话,但为什么例(1a)-(1d)中的句子都能说呢? 1.4 本文的目标 经过上述说明,我们看到同语式在句法上和语义上都面临困境,为了解决上述问题,我们打算引入语义学中有关理性意义和内涵意义的说明,对同语式做出一种新的分析。 二 词的理性意义和内涵意义 2.1 词的理性意义(外延意义) 在哲学家关心的“指称”问题中,外延(denotation或extension)和内涵(connotation或intension)是其中的一对重要概念。徐烈炯(1995:17)转引了Alston关于“外延”和“内涵”的定义: (5)词W的外延式C=C是能真正称得上W的所有事物构成的类。词W的内涵是P=事物具有P性 质是能正确地用W来称它的充要条件。 徐烈炯(1995:17)以“铅笔”为例进行说明:“铅笔”的外延是一切可以被称为铅笔的实体,例如:我的红铅笔,他的中华绘图铅笔,自动铅笔和进口铅笔,等等。而“铅笔”的内涵主要是指铅笔的性质,如它是一种书写工具,主要制作材料是铅。这种内涵规约了词的外延,也就是说,一个东西算不算“铅笔”得看它是否具有上述内涵。Leech(1983)将这种规约外延的内涵看成是外延意义,也就是常说的理性意义。怎么来限定词的理性意义就成了一个大难题。 对意义进行分析从古到今都是语言学界的一个大难题。如果我们要描述一个词的意义,很容易陷入无法停止的循环状态,比如说我们要解释“木头”,就要用到“木材”的定义;要解释“木材”,就要用到“树木”的定义;要解释“树木”,就要用到“树”的定义;要解释“树”,就要用到“植物”的定义。这样无限的循环下去,我们始终无法能够准确地捕捉到意义。 为了更好地描述词的意义,避免词义解释中的无限循环,结构主义和生成词库理论把语义特征看成是一种元语言,并用它作为表述词义的基本单位。持这种观点的语义学,被看成是结构语义学。一般来说,一个词的意义反映的是一种概念,而结构语义学认为所有的概念(也就是意义)都可以被分解成若干个更小的语义特征,通过一定量的语义特征的组合便可确定意义,而这些特征都是二元性的,要么取正值,要么取负值,因此,在结构语义学看来,概念最终是由真值条件(truth condition)决定的。这也正是真值条件语义学所取的立场。例如,如果对某些名词进行语义特征分析,可表述为:
如果例(2a)中前后两个“张三”指的是同一个人,那么这个句子是不成立的,正确的说法应该是“张三打了自己”。例(2a)要想成立,前后两个“张三”必须不同指,如例(2b)所示。 那么,例(1a)-(1d)是不是违反了约束理论呢?以例(1b)为例,前一分句中的两个“科比”分明有同指关系,又显然在一个约束域内。例(1b)这种同语式在生活中并不少见,这显然给约束理论出了一道难题,难道约束域要被重新定义? 1.3 同语式与重言 “同语式”在语义学上还有另外一个名称,即“重言句”。重言(tautology)是逻辑学上的概念,宽泛地讲,是指任何情况下都成立的某些表述。用命题逻辑的术语来说,如果某一命题P永远都为真命题,那么这个恒真命题P就是重言式,所以重言式也被称为永真式。例如: (3)a.现任美国总统是奥巴马,或者不是奥巴马。 b.一加一等于二。 假设例(3a)整个句子为命题P,前一分句为命题Q,那么例(3a)可以被表述为“Q∨-Q”,在析取关系中,无论Q取真值还是假值,整个命题P的值都为真。 不过,对于重言还有另外一种狭义的理解,指的是简单的同义反复,也叫赘言,也就是相同的词语在判断句中反复出现。例如徐烈炯(1995:13)举出这样的例子: (4)启明星就是启明星。 例(4)根本不含有新的信息,在语义上形成了一个悖论。我们把例(4)这种同义反复的句子看成是狭义的重言式。按道理说,一个句子应该包含新的信息,否则就是废话,但为什么例(1a)-(1d)中的句子都能说呢? 1.4 本文的目标 经过上述说明,我们看到同语式在句法上和语义上都面临困境,为了解决上述问题,我们打算引入语义学中有关理性意义和内涵意义的说明,对同语式做出一种新的分析。 二 词的理性意义和内涵意义 2.1 词的理性意义(外延意义) 在哲学家关心的“指称”问题中,外延(denotation或extension)和内涵(connotation或intension)是其中的一对重要概念。徐烈炯(1995:17)转引了Alston关于“外延”和“内涵”的定义: (5)词W的外延式C=C是能真正称得上W的所有事物构成的类。词W的内涵是P=事物具有P性 质是能正确地用W来称它的充要条件。 徐烈炯(1995:17)以“铅笔”为例进行说明:“铅笔”的外延是一切可以被称为铅笔的实体,例如:我的红铅笔,他的中华绘图铅笔,自动铅笔和进口铅笔,等等。而“铅笔”的内涵主要是指铅笔的性质,如它是一种书写工具,主要制作材料是铅。这种内涵规约了词的外延,也就是说,一个东西算不算“铅笔”得看它是否具有上述内涵。Leech(1983)将这种规约外延的内涵看成是外延意义,也就是常说的理性意义。怎么来限定词的理性意义就成了一个大难题。 对意义进行分析从古到今都是语言学界的一个大难题。如果我们要描述一个词的意义,很容易陷入无法停止的循环状态,比如说我们要解释“木头”,就要用到“木材”的定义;要解释“木材”,就要用到“树木”的定义;要解释“树木”,就要用到“树”的定义;要解释“树”,就要用到“植物”的定义。这样无限的循环下去,我们始终无法能够准确地捕捉到意义。 为了更好地描述词的意义,避免词义解释中的无限循环,结构主义和生成词库理论把语义特征看成是一种元语言,并用它作为表述词义的基本单位。持这种观点的语义学,被看成是结构语义学。一般来说,一个词的意义反映的是一种概念,而结构语义学认为所有的概念(也就是意义)都可以被分解成若干个更小的语义特征,通过一定量的语义特征的组合便可确定意义,而这些特征都是二元性的,要么取正值,要么取负值,因此,在结构语义学看来,概念最终是由真值条件(truth condition)决定的。这也正是真值条件语义学所取的立场。例如,如果对某些名词进行语义特征分析,可表述为: