论合成复合词的逻辑形式

      1 引言

      本文探究汉语词法中一个很细微的现象：语法系统应该如何来表达合成复合词中的题元关系。之前的研究发现，汉语合成复合词中的施事题元有时候会跟词结构不对称。（He 2004、2006；何元建2004；何元建、王玲玲2005）这在其他语言（如英语）里也存在。如何处理这种情况，之前对英文的一些分析都不太理想，如Hale & Keyser(1993)、Lieber(1992)，也未涉及汉语。He(2004)虽提出合成复合词的题元关系可以用逻辑形式来表达，但尚未做出详细的论证。在此，本文提出有关论证，结论是：汉语派生功能较弱，其合成复合词中的题元位置大多与表层结构相符，但仍有一少部分需要用逻辑形式来表达，让一个上位的零运算子约束下位的施事题元；英语有很强的派生功能，许多合成复合词的施事题元是一个词缀，词结构跟题元关系不符，也需要零运算子来约束。两种语言都为合成复合词的题元关系可以用逻辑形式来表达这一观点提供了证据。理论上，合成复合词的逻辑形式需要从词库输出，随句子结构进入逻辑形式库得以诠释。这对语法系统的运作，尤其是词库跟句法和逻辑形式库的连接有一定的启发。下面先说何谓逻辑形式，然后分析汉语合成复合词的逻辑形式及其证据，最后是结语。

      2 何谓逻辑形式

      逻辑形式这个概念在扩充的标准理论中就已经有了(Chomsky 1981，1982，1986)，在最简理论中维持不变(Chomsky 1991，1993，1995，2000，2001，2002)。要强调的是，逻辑形式是语法的一部分，是代表句子语义（尤其是逻辑语义）的成分结构(constituent structure)，而不是逻辑学家所说的逻辑表达式。很多时候，句子的表层语序跟它表达的逻辑语义是一致的，例如：

      (1)（所有）发光的不都是金子。

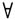       例(1)形式化的表达方法如：“x，～P(x)”，其中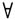，＝全称量词，x＝发光的，P＝谓词（＝都是金子），～＝否定。逻辑上，否定词要出现在被否定的数量词前面。这里，“不”出现在“都”的前面，语义上否定后者，因此这句话的逻辑语义很清楚。即“设X代表所有发光的东西，但X不都是金子”。比较形式化的表达方法就是“x，P(x)”，即所谓的谓词逻辑。

      不过，要不要用这样形式化的方法来表达句子的逻辑语义对分析句子的成分结构本身并不重要，也没有直接关系。另外要注意的是，例(1)中“所有”也是数量词，但它修饰“发光的”，结构上跟谓语中的否定词没有关系，因此不影响句子的逻辑语义，正因为如此，“所有”是可选的。因为否定词跟被否定的数量词之间的相对语序跟逻辑语义不矛盾，所以，例(1)的语序跟语义是统一的。

      不过，句子语序有时跟语义却不一致。例如：

      (2)All that shines is not gold.

      例(2)英文的意思跟上面的汉语句子完全一样，但是英文的否定词“not”却出现在被否定的数量词“all”的后面。语义上，not＝不，all＝所有的；但是结构上，“all”是代词，受关系语句“that shines”（发光的）的修饰；所以，在表层语序上，“all that shines”（所有发光的）被否定了，意思似乎是“所有发光的不是金子”。但这并不对。换言之，说出来的话跟表达的意思有出入，或者说这里出现了句法和语义的不对称。如何解决这个矛盾呢？

      普遍语法理论的途径是通过语法自身的系统来处理这样的矛盾。理论上，语法系统有四个组成部分：词库、句法、逻辑形式库、语音形式库。词库向句法输出词项，句法将词项组成说话人想说的句子的成分结构，这个成分结构再从句法输出到语音形式库，赋予发音相似体(phonetic analogues)，同时也输出到逻辑形式库，赋予语义相似体(semantic analogues)。获得发音相似体的成分结构就叫作语音形式(Phonetic Form)，而取得语义相似体的成分结构就叫作逻辑形式(Logic Form)。语音形式被输送到发音——听声系统，变成指挥发音器官的指令，就得到发音；逻辑形式被输送到概念——意旨系统，获得释义。语音形式库和逻辑形式库分别跟发音——听声系统和概念——意旨系统相连接，所以又叫作语法界面(interface)。原则上，如句子语序跟语义是统一的，那么，它的句法结构跟其逻辑形式也是一致的；如不统一，结构跟逻辑形式也就不一致。那么，当句法结构进入逻辑形式库之后，就会做出相应的调整，使其符合所要表达的逻辑语义。所谓调整，就是成分移位。

      以逻辑运算子(logical operator)为例。逻辑运算子指在句域(domain)中表达逻辑语义的词项，如否定词、数量词、限定词等。这些词除了本身的词汇意义之外，在句子中出现时，还都有逻辑意义，跟出现的句域有关。这个“表达逻辑语义的句域”称为辖域(scope)。拿否定词为例。否定词必须出现在被否定的数量词的上域，即前者的结构位置比后者要高，或者说前者统制了(c-command)后者。在例(1)里边，这的确如此，如：