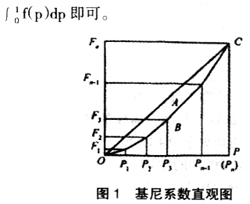
中图分类号：O212.1 文献标识码：A 文章编号：1002－6487（2008）06－0079－03 我国关于教育公平的研究多停留在现象描述阶段，缺乏相关理论和方法指导的经验研究，这既是由于选择度量教育差距工具的困难，又是因为相关数据的匮乏。为了解我国教育公平的整体状况，分析教育资源配置的公平程度，制定有效的教育资源配置政策，我们亟需界定和度量我国的教育公平程度。本文将采用教育过程中的教育经费指标考查我国教育资源配置的公平状况，因为优化教师配置和改善办学条件都离不开教育经费的保障，教育经费本质是投入教育领域资源的货币表现，因此教育经费指标反映出的教育公平更具整体性和现实性。 1 研究综述 作为一种常用的统计分析方法，基尼系数是广义的分析工具，不仅可用于收入分配问题的研究，而且可以用于一切分配问题和均衡程度的分析。基尼系数（也称基尼集中比率）是用来描述财产、收入、人口、种族、犯罪、教育等社会状况集中程度的量。它的值在0～1之间，0表示无集中，完全均等，1表示最大集中程度。一般认为，0.4为集中程度的警戒线，如果某一社会状况的基尼系数超过0.4，则表明集中程度已经很高，即达到了非均衡状态。当前，国际上对教育公平程度的测度指标多采用教育基尼系数，并已开始应用于跨国分析[1]。本文选择教育基尼系数作为衡量中国教育公平程度的工具，并用洛伦茨曲线进行直观的图形说明。 1.1 数据单位形式 从最初含义来看，基尼系数表示的是任何一对样本收入差的绝对值[2]，理论上应以每个人的收入为考察对象，同理，我们研究教育基尼系数的目的是分析教育资源在适龄学生的分布公平状况，应以每个适龄学生获得的教育资源（生均教育资源）作为考察对象，以人均教育资源作为分析对象人为改变了教育资源的实际分布，也不易问题的说明和解释。 此外，统计部门公布的教育数据多为分组汇总后的数据，原始的微观数据多不可得，在计算基尼系数时，必须要注意到分组数据的计算结果存在误差，因为组内差距往往被忽视，或者对组内的分布进行假定，这都会造成估计上的一定误差。[3]我国公布的教育数据多停留在省市区一级，这样必然掩盖了省域内部，以及城乡之间的差距。 此外，另外值得关注的是，教育经费相关数据以货币单位度量，存在着物价变动因素，因此在计算教育公平尤其是教育经费公平的时间动态变化时需要剔除物价变动因素，并且由于各地物价水平变化不一，应把各地的教育经费按照各自的物价水平予以剔除，但国内相关研究基本未考虑此类问题。 1.2 计算方法选择 自基尼系数产生至今，其计算方法已经发生了很大变化，目前常见的就有几何法、平均差法、协方差法和矩阵法等。各种方法内部又区分为多种不同的详细计算方法，各种方法计算的结果也不完全相同。因此，如何根据比较研究探询一种适合我国国情和教育现状的计算方法尤为重要。 基尼系数可以通过图示进行最直观的理解。图1中的正方形边长为单位1，横轴和纵轴分别表示按收入高低排序后的人口累计百分比和对应的收入累计百分比，对角线OC表示绝对平均线，折线OPC表示绝对不平均线，实际曲线位于上述两条线之间，越接近对角线OC表示收入分配的差距越小。基尼系数也就表示为图中区域A和区域（A＋B）两部分面积的比，即G＝SA／（SA＋SB）＝2SA＝1－2SB。从计算SB的角度看，大体上可分为离散方法和连续方法两种，前者即计算洛伦茨折线下一系列小梯形（含小三角形）的面积之和，后者即用一个函数f（p）来拟合洛伦获曲线，然后计算
尤其要提到的是，通过各种离散公式计算的基尼系数值都是相等的（不考虑结果的精确度），它们其实都是SB计算过程的不同步骤或表现形式。计算基尼系数比较常见的公式有：
采用连续方法估计基尼系数最大的不确定性是采用何种形式的函数拟合洛伦茨曲线，由于满足洛伦茨曲线性质的待选函数很多，采用不同函数估计基尼系数肯定有出入，而且有时还相差较大。可能是各个学者对拟合函数的偏好不同，国内经常看到只用某个不加说明的特定函数测算基尼系数的文章，应该说这也是造成国内基尼系数值泛滥的一个原因。 1.3 教育指标判断 教育机会、教育过程和教育结果在基尼系数的计算上存在较大的差别，以教育结果为例，它的基尼系数反映教育程度在各组人群中的分配公平程度，但无法反映不同教育级别的公平程度，尤为重要的是，由于该指标的基尼系数必须以历年各学历程度的人口存量为基础，而到目前为止我国并没有此项专门、完整的统计数据，因此该数据均为各学者的估算，缺乏统一和客观的标准。比较而言，教育机会和教育过程的数据多为已公布的统计数据，在计算上更加令人信服。由于上文所说的教育机会基尼系数研究的问题，本文最终选取了教育经费作为分析教育基尼系数的指标。
