分形美学在建筑设计中的运用

      中图分类号：TU－8 文献标志码：A 文章编号：1009-1971（2008）05-0022-05

      自然界中，反复出现而又变化无穷的事物和现象令人振奋和迷恋。连绵的山峦、蜿蜒崎岖的河流、瞬息万变的云朵等等，种种美丽的形态在令人感到熟悉的同时又是那样的出人意料，自然的特质赋予了人们在艺术创作中无尽的遐想（图1）。

      

      图1 木星的表面

      历史上，艺术是人类对自然世界体验的结晶。无论建筑还是装饰艺术无不散发着对人们对自然的崇拜和质朴的美。从古至今先人创造了无数的艺术精品并用自相似性揭示着生命精神与自然产生的共鸣（图2）。建筑与自然的和谐关系一直是人们研究的课题。如何使建筑更加地接近自然、融入自然之美也一直是许多建筑师所追求的方向。

      

      图2 不同历史时期的装饰艺术图案

      一、朴素的建筑自然观

      美国现代主义建筑大师F·L·赖特在崇尚自然的建筑观方面极具代表性，并在其建筑作品反映出对自然的深刻理解。在他的心目中，建筑不是固定的形态，而是要如同自然万物一样，强调局部与整体的相互依存，强调不断地发展进化。在《论建筑》一书中他写道：

      “大自然为建筑的设计提供了素材，我们今天所知的建筑形式来源于大自然。尽管几百年来，人们总是在书本上寻求启示和死守教条，但大多数成功的实践还是来源于自然。自然的启示是取之不尽的，它的富有超乎人们的想象……对建筑师来说，没有比对自然规律的理解更为丰富和更有启示的美学源泉了。……当‘自然’这个词被理解和接受时，我们就不会对创造能力的问题有所疑虑了。‘独创性’变得自然而然，因为人们已经站到了一切形式的源头。”[1]

      如果说赖特朴素的自然建筑观来源于他对自然事物表象的热爱、探索和模仿，那么，随着数学家曼德勃罗分维几何理论的开创，则使人们能够更深刻地认识到纷繁复杂的自然事物背后的美学规律，从而为建筑设计开拓更加广阔的视野（图3）。

      

      图3 赖特设计的西塔里埃森

      二、分形理论的发展历程

      分形理论是科学家用以描述自然事物混沌特质的几何学理论。这一理论是几代数学大师的智慧和钻研的结晶。

      在经典几何学中，已经习惯于欧几里德几何的思维与表达方式。人们通常自然地假定：线段是笔直的，四边形是规则的，木材的密度是均匀的，圆球体的表面是光滑的。在这些假设下就可以用一个整数去表征一个图形的维数，即大家熟悉的所谓一维线段、二维平面和三维空间等概念，这里都利用了欧几里德几何学原理。但是，当人们对一些复杂事物进行描述和组合时，就会发现欧几里德几何并不能真实地反映事物的本质特征。

      1883年，德国数学家康托（G.Cantor）构造了一个奇异集合：取一条长度为1的直线段E0，将它三等分，去掉中间一段，剩下两段记为

      E1，将剩下的两段再分别三等分，各去掉中间一段，剩下更短的四段记为E2……，将这样的操作一直继续下去，直至无穷，得到一个离散的点集F（图4），称为康托尔三分集。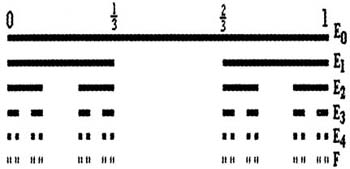

      

      图4 离散的点集——康托集合

      1915—1916年，波兰数学家谢尔宾斯基（W.Sierpinski）将三分康托尔集的构造思想推广到二维平面，构造出谢尔宾斯基“三角”：设

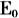      是边长为1的等边三角形区域，将它均分成四个小等边三角形，去掉中间一个得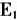，对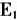的每个小等边三角形进行相同的操作得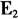，……，这样的操作不断继续下去直到无穷，所得图形F称为谢尔宾斯基“三角”（图5）。