语言学中的概率思想由来已久。1960年代以前，语言学研究中占主导地位的是基于统计分析的概率性研究。但此局面被Chomsky(1957)所倡导的生成语言学所改变，与当时计算科学的发展相对应，其理论核心是非概率性的模块论，此理论模式一直延续到最简方案 (Chomsky and Lasnik 1995)，其基本算法是离散性概念的线性推导。Chomsky和Halle(1968)发表的《英语音系》(Sound Pattern of English,SPE)一书，是该潮流在音系学中的表达。正统生成语言学（包括生成音系学）认为能力与表现，或者说语言知识和语言行为之间有不可逾越的界限，同时认为音系和语音之间，或者说言语者的隐性音系知识和他们的实时处理技能之间泾渭分明，并将所有统计学意义的变异都归因为表现而非能力，因而难以解释语言习得和自由变异。然而，现代音系学中另外一种倾向正变得越来越明显，其基本理念是音系知识和语音处理之间是共生的、相互依存的关系，是同一完整系统的两个方面(Pierrehumbert 2001a:137-57)。优选论(Optimality Theory,OT)的最新发展就是该倾向的突出代表。 1990年代初推出的OT和生成音系学有很深的渊源。经典OT继承了生成音系学的深层表征和表层表征的区分，在这个意义上，它仍然是推导性的音系理论。但经典OT还继承了非线性音系理论的各音层相互独立的思想，抛弃了SPE以来的规则串联有序推导，不改变底层表征，通过对表层表征施加并行评估，而获取优选输出项（马秋武、王嘉龄2001:F27）。与计算科学的新发展相对应，其创始人Prince和Smolensky(1993:3)则认为OT可以通过连接主义网络得到最好的体现。OT的最新进展表现出对功能主义的日益注重，主张语言习得的基础是语言经验，使得该理论更符合人类认知的特点(Kirchner 1997:83-111；王嘉龄2002:30-4)。OT的另一进展表现在学习演算系统的建设上，并研发了专门的运算软件OTsoft(Hayes et al.2003)。这些进展从根本上说都有赖于对概率性语言学研究传统的回归。 1.概率性优选论的理论前提 当代认知科学的一些基本假设为概率性OT提供了理论前提。 假设1：语言是人类认知系统的一部分(Ciere 1987:139-59)。 假设2：认知就是对输入进行表征，就是符号化表征的建构和处理，也即编码(Hale and Reiss 2003:219)。 假设3：某些语言结构直接在认知系统中进行编码，有些则只是间接地在认知系统中获得编码(Goldrick 2002:3)。 假设4：言语产出概率可以同时受多层表征的制约(Goldrick 2002:22-31)。 假设5：由于输入信息包含噪声，且认知资源有限，人类认知是对有限认知资源优化利用的概率性过程(Anderson 1990)。 假设1和假设2实际上暗含着一个推理，那就是，语言作为认知表征不等于认知的对象。用语言哲学家Frege(1892)的话说，语言只是对客观对象(objects)的描述，一个描述指示一组客观对象，但该描述的具体程度永远都不足以确定其中任意一个。因此，就音系学而言，一个公理性的基本假设是，所有音系表征本质上都是源于语言实践对真实世界中话语的描述，是基于语言经验的“随机密度分布”(stochastic density distribution,Pierrehumbert 2001a:137)。在这个意义上，可以说，传统生成音系学的问题就在于从一个对真实对象的描述直接推导出了客观对象(Bid 1996:32)，忽视了音系及其语音实现中概率特征的作用。Pierrehumbert(2001b:195)指出，任何层面的音系知识都与语言处理的概率模型相关联，在不同的音系或语音抽象表征层都发现存在着概率性效应。人们对语音空间（注：空间本身是一个概率概念，从概率统计的角度出发，“空间”即在满足一定条件的情况下，某一函数的所有可能取值的集合。）和音系概念的连接具有概率性知识，或者说，人们通过概率性的知识来联系语音空间和音系概念。概念相互组合构成词库中的词项，词项与词项之间又以特定方式相连接，人们对此类组合和连接的频率也具备概率性的知识。因此，音系表征与语音产出的关系必须通过心理表征在语音空间中的概率分布来描述。 假设3实际上区分了语言结构在认知系统中的不同层面。具体地说，关于任何一个语言学理论，至少可以区分两类描述：结构性描述全集和外显结构性描述(Tesarand Smolensky 1998:236)，前者指基于某特定理论的所有可能的结构性描述；后者是指学习者可直接处理的描述，是前者的一个子集。 根据假设4，可以认为产出音系可以同时受语音制约条件和音系制约条件的制约。 基于假设1到假设5，语言处理作为一个认知过程，可视为一个函数，该函数对输入表征与输出表征的映射分配概率。设输入I和输出O都是可数非空集，那么二者的映射I×O也是可数非空集，设所有合法的或者说符合某一理论结构性表达要求的映射为C，那么G
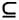
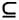I×O。这样我们就可以定义一个输出项：
