宋词阳声韵的数理统计分析

      中图分类号：H113　文献标识码：A　文章编号：1000-1263(2005)01-0082-07

      一

      研究诗文用韵，判断通押和合韵时，通押比例是一个最重要的数据。在实际操作过程中，主要的问题是通押到何种程度算合韵？各家学者存在很大的分歧。朱晓农先生就此问题做过详细讨论[1]p10-20。

      早在上世纪三十年代，陆志韦先生就开始使用几率相逢数来研究《广韵》的声母[2]，自此数理统计法逐渐开始应用于音韵学研究，白一平先生使用卡方检验法考察了诗经幽部字*u，*iw两韵的合用问题[3]，朱晓农先生使用t检验法讨论北宋中原地区词人的用韵[1]，麦耘先生在朱晓农先生公式的基础上编制了电脑软件，检验分析了隋代的诗韵材料[4]。

      1.1　判断合韵与否的主要依据是通押比例，根据比例来判断通押是一种随机现象，还是一种经常的行为。为了判断随机通押与经常通押的区别，我们需要建立一个这样的数学模型：假设有A、B两韵字，A、B两韵随机通押概率相当于从所有韵字中随机取两个字，恰好一个是A韵字、一个是B韵字的概率（记作1）。然后我们将韵段中A、B两韵实际通押次数与全部韵段的比率（记作R）计算出来，将R和I做一比较。如果R超过I较多，可以说两韵的通押是经常的；如果R比I小很多，那么两韵的通押是随机的；如果R和I差不多，则使用假设检验法来帮助我们判断。

      在数理统计法使用以前，一般讨论通押比例皆以韵段为单位，只计算R的值，到百分比为止。韵段的单位过于粗疏，例如同是臻梗通押的两个韵段：王观《高阳台·红人桃腮》（一262)：分臻孙臻闻臻人臻轮臻云臻名梗春臻（注：韵例说明：首列作者姓名，书名号内是词牌及首句，首句超过4字的只取前4字以节省篇幅，括号内大写数字是卷号，B表示补辑，阿拉伯数字为页码。版本用中华书局1980年《全宋词》繁体竖排本。）。杜安世《玉阑干·珠帘怕卷》（一172）：景梗尽臻径梗信臻定梗趁臻。他们所表达的臻、梗合用的关系是不同的，后者更能反映出两摄的密切关系。如果以韵段为计量单位，他们都算1次，抹杀了后者所反映的意义。白一平先生用马尔柯夫链作为计算押韵的基本单位，朱晓农先生称之为“韵次”，初步解决了区分韵段中韵字多寡不同、位置各异的问题[1]p7-10。

      　但是，这种方法只计算相邻韵脚押韵，而把非相邻韵脚之间的关系排除在研究视野之外，不能反映三韵以上同用的关系。例如，刘辰翁《清平乐·深红半面》（五3195）叶：唇英承。是二个谆庚蒸三韵同用的韵段（举平赅上去），韵次有两个：唇英（谆庚同用）、英承（庚蒸同用），而谆蒸同用没有体现出来，割裂了不相邻的韵脚“唇”和“承”之间的关系。因此，我们定义一个新的计算单位：韵段中每两个韵字两两组合称作为1韵组。用公式表示就是：

      

      公式①计算两个韵部j、k之间关系的辙离合指数，公式②③计算两个韵a、b之间关系的韵离合指数。公式①除号以前的数值代表j、k韵部实际相押的比率，后面括号内的数值代表理论上随机相押的比率。这个随机相押的比率是通过排列组合原理得出来的，有个形象的比方，就是从总数为Z的球袋中摸球，第一个摸出是标签是j的球的概率为Zj/Z，第2个摸出标签是k的球的概率则是Zk/Z-1。这样两个球恰好前j后k的概率就是两者的乘积，同理再加上两个球前k后j的概率，就构成了i、k两辙随机相押的总概率。公式②③朱晓农先生未多加解释，但似乎和公式①略有不同，被除数仅是a、b两韵的总字次和总韵次，而把同一个韵段中a、b韵和其他韵组成的韵次置之不理，无形中可能放大了概率，不符合排列组合的精神。两个公式既然是从同一个原理推导而来，应该算法相同较为恰当。因此我们将韵离合指数的公式修改为：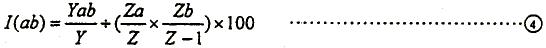

      

      这样，公式④和公式①的原理保持一致（因为韵组是组合而来的，这里我们也用组合，不用排列，所以不乘于2）。将所有含有a韵韵字或b韵韵字的韵段作为样本，Y指样本的总韵组，Z指样本的总字次。当I(ab)＜50时，认为ab两韵应分开，当I(ab)＞=90时，认为ab两韵应合并，当50＜=I(ab)＜90时，需要进行假设检验（注：I(ab)的两端是50和90，为什么是这两个数字，朱晓农先生没有详细讨论，看来是一个经验值。）。

      1.3　使用假设检验的前提是首先要保证样本有足够的数量，宋词用韵样本数（韵段数）大多在几百以上，多的甚至达到上千，符合这一要求。有些学者在某个词人总的词作才几十首、全部韵段不过百多个的情况下使用数理统计法，其结论不能不让人感到怀疑。虽然t检验是适用于小样本分析的方法，但是对样本的数量仍有一定的要求，当原始数据量较小时，结果的可靠性就很差。麦韵先生特意强调，对于字次小于10的韵，即使它与别韵的离合指数在50到90之间，也不再进行t假设检验；两韵互押不到5次的，也不做检验[4]p115，这种做法是比较科学的。

      其次，样本的分组影响数据的分布。诗文用韵研究中的样本是韵段中通押韵组与该韵段全部韵组的比率。比方说我们考察宋词韵里面侵韵跟真韵的关系，首先把含有侵韵或真韵的韵段搜集一起作为样本，一共有1930个。可以分为两类：一类是侵真合用的韵段，有211个，如苏轼《江城子·腻红匀脸》（一329)：唇谆新真春谆颦真人真阴侵深侵心侵今侵，这个韵段中侵真合用韵组12个，全部韵组36个，那么比率就是0.3333；另一类是非侵真合用韵段，有1719个，如柳永《甘草子·秋尽》（一15）：尽真粉信真紧真嫩顿恨，晏殊《浣溪沙·三月和风》（一88）：林侵金侵阴侵心侵深侵。这类韵段侵真合用韵组为零，因此比率都是零。如果我们直接以每个韵段的比率作为样本，那么大部分样本都是零，这样的样本呈偏态分布。偏态分布可以利用box-cox公式模型化为正态分布，但是无疑影响统计的结果。