0 本文的宗旨 从《马氏文通》开始经过90多年的研究,汉语语法中仍然有许多基本问题未能解决。为了解决这些问题,也为了给汉语语法奠定坚实的理论基础,有必要屏除一切先入之见,从零开始进行细致的元理论分析,弄清语法的本质是什么,语法中必要的概念是什么,各种概念之间有什么依存关系,可能采取的工作方式又是什么。 元理论分析必须从一定的假设入手。本文的论证思路是,首先提出语法的一种定义。这种定义规定了语法的样式,或者说规定了语法模型的一种类型。然后分析在这种定义中假定了哪些东西,那些东西之间可能有什么关系。结合具体的语言材料和语法学者的一些观点,研究可能进一步引入怎样的一些假设,推演从每一种假设可能得出的结论和可能采取的工作方式。 需要说明的是: 1.在元理论分析中,逻辑关系特别是公理系统的一致性是仲裁。任何观点都只是假设,没有先天的权威性。即使是公认的观点,不管它有多么悠久的历史,只要它跟另外一些已被论证所肯定的观点矛盾,就必须修正。 2.元理论分析要求有系统性,不能断章取义。一种观点可能在某些假设之中成立,在某些假设之中不成立,这跟它本身对不对无关。要肯定或否定一个观点,就要拿出一个论证系统来,不能贯串成系统的东西无所谓对不对。所以不能孤立地讲哪种观点可行,哪种观点不可行。 3.元理论分析肯定公理系统有多样性。本文只是试图研究为汉语建立语法模型可能采取的一种方式而已,不排斥其他的方式——事实上目前汉语语法模型是太少而不是太多。但是一切语法模型在宣告自身的存在时,都不能不考虑要不要具有系统性。不要系统性、只作零散的局部描写也未尝不可,但是不能否认当前缺少的是具有系统性的汉语语法模型。 4.本文是关于汉语语法元理论研究报告的选段和缩写。限于篇幅,既不能铺陈语料,也不能全面论述。为了保证有一定的可读性,尽可能不使用技术性的语言,也尽可能简化论证过程。文中语句不详之处,可参看笔者的其他文章。 5.本文从语法的定义开始推理,文中出现的某些命题虽然以往有人提过,但不是以这种论证方式提出来的。所以在本文的论证中肯定或否定的论点在别的场合不一定成立,也不一定不成立,对此本文不打保票。为防引起误会,一般不注出处。 1 语法的定义 1.1 从传统的定义开始 在语言学中,语法可以有多种定义,包含的内容也可以有很大差异。不同语法理论或语法模式的共识是语法描述使用语言中的小单位构成大单位的方式,差异则主要体现在(Ⅰ)语法中的小单位和大单位是什么东西,(Ⅱ)怎样描述用小单位组成大单位的组合过程。如果求同存异,那么下列传统语法定义所研究的内容仍然是目前各种语法模式的核心部分——至少也是重要的基础。 定义G:语法研究词形变化的规则和用词造句的规则 1.2 语法规则 我们把由定义G确定的语法模型叫作语法模型G。根据定义G,模型G中包含的语法规则(R)有两种类型: R[,1]:W→W['] R[,2]:{W[,1],W[,2],…,W[,n]}→P R[,1]是词形变化规则,说明怎样由词W求出它的变化形式W['];R[,2]是用词造句规则,说明怎样由若干个词{W[,1],W[,2],…,W[,n]}组成一个单位P,P可以是一个句子,也可以是由词造句过程中产生的中间单位,但不是词。① 例如,对于汉语动词“吃”而言,它在句子中可能出现“吃了”、“吃着”、“吃过”等形式。如果我们把“了、着、过”看成汉语动词的词形变化成分,那么由“吃”产生“吃了”等形式就可以使用规则R[,1]: 吃→吃了 如果我们把“了、着、过”看作独立的词,那么由“吃”产生“吃了”等形式就可以使用规则R[,2]: {吃,了}→吃了 1.3 弗雷格原理 上述语法规则可能有两层含义:一是形式合成法则:由左边的各个单位的形式按规则进行操作,可以得出右边单位的形式;二是意义合成法则:由左边的各个单位的意义按规则进行操作,可以得出右边单位的意义。尽管未曾明言,但传统语法实践证明它默认语法模型G需要满足这两个条件。在现代逻辑中,则以弗雷格(Frege)原理的形式对此作了明确的规定。本文的一切讨论以此为前提,下文所说每一条规则都同时具备形式和意义两个部分。凡是只讲a和b可以合成ab,而不讲怎样由a和b的意义生成ab的意义的规则不予考虑。 需要注意,在说W[']是W的一个变化形式时,只是说由W的意义可以按一定法则求出W[']的意义,并没有说W和W[']的意义完全相等。正如我们不能说英语动词的现在时形式与过去时形式意义完全相同一样,即使把“吃了”看成“吃”的变形,也不能说“吃”和“吃了”意义完全相同。② 下文把R[,1]和R[,2]合称为造句规则,用R表示。 2 语法中的“词” 2.1 词和句子的三种关系 定义G断言语法模型G中至少包含下列概念:词、句子、词形变化规则R[,1]和用词造句规则R[,2]。这就是说它断言(Ⅰ)语言L中有词(W)和句子(S)两种单位,(Ⅱ)若干词可以遵循一定的规则(R)合成句子。 合成和分解互为逆过程,说a和b可以用规则合成P,其前提是P可以用规则
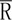
分解为a和b。R和
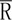
互为逆规则。这显然表明,定义G断言有造句规则R把词组合成句子,也就是断言有析句规则
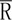
把句子分解为词:有R则有
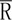
,有
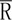
则有R。由此可以得出下列推论:
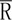 分解为a和b。R和
分解为a和b。R和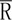 互为逆规则。这显然表明,定义G断言有造句规则R把词组合成句子,也就是断言有析句规则
互为逆规则。这显然表明,定义G断言有造句规则R把词组合成句子,也就是断言有析句规则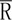 把句子分解为词:有R则有
把句子分解为词:有R则有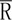 ,有
,有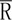 则有R。由此可以得出下列推论:
则有R。由此可以得出下列推论: