教育研究中的多层分析方法

      教育研究在注重理论发展的同时，还应紧密结合教育的实际，把握大量的反映实际状况的资料。近10年来，国际上在教育研究的数据分析方法这一领域有了许多新的发展，其中最值得关注的技术是结构方程模型(Structural Equation Modeling)和多层分析方法(Mutilevel Data Analysis)。结构方程模型近年来已普遍受到国内学者的注意，但多层分析方法在国内教育界尚未引起足够的重视。本文将着重介绍这种方法的背景及优点，以期引起国内学者的讨论和应用。

      在教育研究中，如果仔细分析的话，我们应该收集的数据存在着一种层次的结构。首先是有关学生本人及相关的变量，例如，性别、年龄、家庭环境、父母受教育的程度等等；其次是一组学生的变量，例如，所在班级的大小、男女生的比例等。因为各个学生是在班级里进行教学的，显然一个班级所包含的特征由许多学生的特征构成。班级又组合成学校，同时学校又组合成学区。如此的组合就形成一个不断上升的层次结构。如图所示：

      

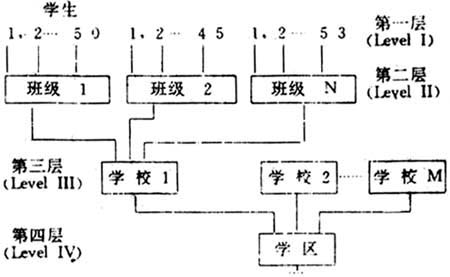      在一个纯实验研究中，我们为了证明某种教育措施的效果，例如教材、教法，研究者需要随机地选择学生并把他们分配在实验组和控制组中，然后收集数据，用方差分析判断实验组和控制组的差异。但是，这种实验在教育研究中实际上是很难做到的。如果我们的数据是在自然状态下收集的话，如果我们研究的问题仅涉及到学生个体及有关的变量时，这种数据结构的影响还不明显。但当我们的研究涉及到两个以上层次数的变量时，选择适当的分析方法反映数据的这种层次结构就变得非常重要了。早在1950年Robinson就提出了对来自不同层次的变量必须采用适当的分析方法的问题。忽视或抹杀数据的这种层次结构，就不能对研究的现象提出客观、准确的解释。近年来多层数据分析模型就是试图解决这方面的问题。所谓多层次就是指在一个系统中的各单位之间的层次的或网状的结构关系。

      一、传统的分析方法

      下面我们简单地回顾一下传统的分析方法。长期以来，我们的做法是试图人为地简化数据的层次结构，要么简单地把在学生水平上的数据以平均值带入到更高一层的分析中；要么是把更高一层的数据分配到每个学生，然后带入分析的过程中去。但是无论如何这样的做法都没有考虑到数据的客观存在的层次结构。

      在过去的教育研究中，对研究对象的层次分析法有三种，都是通过将不同水平的变量放到同一回归方程中作分析。

      1.学生之间的分析

      例如，在学生水平上用学生的性别、民族、父母的职业、父母的受教育程度等因素对学生的学习成绩进行回归分析，以确定各因素对学生学习成绩的影响程度。如果在研究中仅考虑学生自身的特征因素，可以直接不分学校地将从不同学校获得的数据合并，然后用所有学生的数据进行回归分析，获得对学生的整体水平的了解。但如果我们在这种分析中包含了学生变量时就引进了不同层次的变量的分析。传统的做法是在这一种水平的分析中不考虑学生所在的组类的特征差异，将所有学生都合并起来作整体分析。假设有两个自变量，回归分析方程可以表示为：

      Y[,ji]=B0+B1X[,ji]+B2G[,ji]+E[,ji]…(1)

      其中，Y[,ji]表示因变量，X[,ji]表示有关学生特性的自变量，G[,ji]表示有关学校（组）特性的自变量，j=1……J表示学校号，i=1……N[,j]表示组内学生的学生号，B0是截距（相当于平均数），B1和B2是回归直线的斜率（其值的大小反映出因变量随自变量的变化而变化的程度），E[,ji]表示随机误差项。需要注意的是，在这一方程里，某个学生组水平变量G[,ji]实际上等于G[,j]，也就是说对来自同一组内的学生重复使用了同一具有相同值的变量，这种做法是有问题的。由于将同一学校的数据纳入学生水平对该校的学生进行重复使用，当学校水平数据的差异极小或为零时，使得分析失败；而当学校水平的数据稍有一点差异时，这一些变量又会不可避免地累加出很大的差异，使分析结果出现一些严重而且无法进行解释的显著性差异。

      2.学校或班级间的分析

      在这类研究中仅考虑学校、班级（组）或以其它用于分组的因素特征对学生成绩的影响。其分析的方法变化为：将学生的学习成绩以学校为单位计算各个学校的平均分，再用学校的特征因素，如学校的地域因素、师资因素、规模因素等对学生学习成绩进行回归分析。

      Y[,j]=C0+C1X[,j]+C2G[,j]+E[,j]……（2)

      其中，Y[,j]、X[,j]都是从方程(2)的Y[,ji]、X[,ji]以组为单位求平均数获得的，G[,j]本身就是以组为单位记录的，不做变换。

      这种分析方法对数据作了求平均数的变换，获得的结果也不太可靠。这是因为如果以学校或其他分组的形式求组的平均分，平均分本身就丢掉了许多信息。最主要的一点是反映各组（学校或班组）学生的成绩差异的标准差不能被纳入回归方程中进行分析。假如我们研究的对象是来自100所学校的5000名学生的情况，并已获得了每个学生的学习成绩，而在进行学校水平的回归分析时我们只用了100个学校水平的学生平均成绩，这种变换数据的做法会由于增大数据的标准差或忽视取样的不足而使所获得的统计结果很不可信，并能产生差别很大的结果。另外，将有关学生的数据转换为以学校为单位的平均数进行分析，这种做法也往往偏离了研究者对所感兴趣的目标的分析。许多研究的对象是学生而不是学校，学习是学生的行为，不是由学校完成的，因此我们不能仅仅根据学校水平的平均数来对学生的学习成绩作解释。使用学校水平的学生平均数进行分析，获得的结果对现实情况的解释并不能提供有效的帮助。