ⅩⅤ 170、集合论认为, 真正无限的东西不可能用算术符号体系来表示,它只能描述而不能表示。就像人们可以谈论一种结构,而不必用命题本身来表达它。这种方法如此处理每一个概念,以至于使它的形式消失了。 171、一个函数的持续性的所有证明都必然要涉及到一种数制。 主要在函数运算中表现出来的数字阶梯,是不会在一般性的观察中消失的。——持续性是否可以被描述?一种形式不可能被描述而只能被表示。 172、 “一条曲线的最高点”并不意味着“这条曲线上所有点中的最高点”。同样,一个函数的最大值不是所有值中的最大的值。而是,我可以构造最高点,也就是说,从一个规则中得出它。 173、当仅以前行中的无限可能性为前提时,“(n)…”这一表达才有意义。——布劳威尔(Brouwer)。——狄得金德式划分的解释, 好像它是直观的;或者R有最后一节,L有第一节,或者其它等等。实际上这些情况中任何一种都无法想象。 174、集合论(Mengenlehre)是建立在假设的符号体系、亦即谬论之上的。就好象在逻辑学中有一些我们不可能知道、但又是可知的东西。——当人们(如布劳威尔)说,在(x)·φx=ψx 这种情况中除了是和否以外还存在着不可判断的情况,这就意味着,“(x )…”被理解为延展的,而且所有的x可能碰巧具有一个特性。 175、假如我们按照罗素的意思把“ψx=0 这一方程的根”视作一种描述,那么用句子“x+2=6 这一方程的根”所表述的意思肯定不同于说等于4这样的句子。 176、 单纯内在的一般性怎么能由于一种个别情况(即某种外在的东西)的出现而被驳斥呢?但是特殊情况对一般命题的驳斥是出自内部——它反对内在的证明。——x[2]=x·x和x[2]=2x这两个方程之间的差别并不是其正确度的差别。 ⅩⅥ 177、在平面上的一个点通过一个数对来表示, 在三维空间中的一个点通过一个三数聚合来表示,这已经表明,这里所表示的对象根本不是点,而是点的集合。 178、作为句子句法的几何学涉及的是空间中的物体。 在视觉空间中排列成行的东西,是先验地亦即按其逻辑本性处于这种秩序之中,几何学在这里简单地说就是语法。物理学家在物理空间的几何学中使之相互发生关系的东西就是仪表读数,这种仪表读数按其内在本性都是不变的,不管我们是生活在一个直线空间还是生活在一个球体空间。 179、 我可以通过按照投掷硬币所示结果不断取半的方法无限地接近一条直线上的任何一个点。我是否能够以类似于根据投掷结果(头像或鹰)把0或1写成一个无限的二元小数的方式,把有理数分为两类?通过投掷的规定不可能描述出结果的规则;无限的不确定性并不决定数。 180、是否可能在规则中从规则进行抽象, 并且把延伸看作是被表述的本质的东西?——假设我在不存在有理数的地方切断,那么肯定有一个这个切点的近似值。但是趋近谁?在数的领域内暂时还没有一个我可以趋近的东西。——一条线上的所有点实际上可以通过算术定律来表达。在通过连续等分求近似值时,人们通过有理数来接近每个点。 ⅩⅦ 181、说无理数是整体的,对此有什么标准? 每一个无理数都沿着一个有理近似值序列前行,永远不会离开这个序列。如果我有除了π以外的所有无理数的总体,现在把π填入,我却不可能给出一个点是真正需要填入π的,π在每个点上都有一个伴随者。这清楚地表明,无理数不是一个无限小数的延伸,而是一个规则。如果π是一个延伸的话,我们就永远不会经过π——我们永远不可能发现一个空缺。 182、
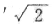
:带有一个例外的规则——必须先有数字规则, 然后在数字规则中表达,比如——一个根。但是数序的这种表达只有在它是一个实数表达时才有意义。假如我们后来再去改变它,那只会把表达搞乱,却不会得出一个新的数字。 183、假如
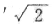
确实有什么意义的话,那就是与

完全一样, 只不过是另一种表达方式;在另一种系统中的表达。
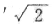
在处于一个系统中之前并没有固定值。对于
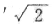
人们不能说,它是这个数序值的极限,就像我们不能说,投掷的规定是投掷结果的极限。 184、人们可以应用规则,这一点也同样适用于投掷数字的规则。把π'与此相区别的只是在于,我们知道肯定存在着一个规则,按此规则在π中会出现数字7,即使我们还不知道这一规则。 π'暗示着一个未知的规则。
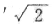 :带有一个例外的规则——必须先有数字规则, 然后在数字规则中表达,比如——一个根。但是数序的这种表达只有在它是一个实数表达时才有意义。假如我们后来再去改变它,那只会把表达搞乱,却不会得出一个新的数字。 183、假如
:带有一个例外的规则——必须先有数字规则, 然后在数字规则中表达,比如——一个根。但是数序的这种表达只有在它是一个实数表达时才有意义。假如我们后来再去改变它,那只会把表达搞乱,却不会得出一个新的数字。 183、假如 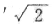 确实有什么意义的话,那就是与
确实有什么意义的话,那就是与 完全一样, 只不过是另一种表达方式;在另一种系统中的表达。
完全一样, 只不过是另一种表达方式;在另一种系统中的表达。 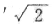 在处于一个系统中之前并没有固定值。对于
在处于一个系统中之前并没有固定值。对于 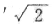 人们不能说,它是这个数序值的极限,就像我们不能说,投掷的规定是投掷结果的极限。 184、人们可以应用规则,这一点也同样适用于投掷数字的规则。把π'与此相区别的只是在于,我们知道肯定存在着一个规则,按此规则在π中会出现数字7,即使我们还不知道这一规则。 π'暗示着一个未知的规则。
人们不能说,它是这个数序值的极限,就像我们不能说,投掷的规定是投掷结果的极限。 184、人们可以应用规则,这一点也同样适用于投掷数字的规则。把π'与此相区别的只是在于,我们知道肯定存在着一个规则,按此规则在π中会出现数字7,即使我们还不知道这一规则。 π'暗示着一个未知的规则。