虚实之辨：论胡塞尔向实然状态的还原

      在《什么是超越论一现象学的还原？——从胡塞尔还原方法的范围问题谈起》①一文中，笔者以“什么是可被怀疑的、什么是不可被怀疑的”问题为线索，初步回答了胡塞尔整个还原操作方法的范围问题。对这一看似简单问题的深入思考，有助于相对容易地进入胡塞尔现象学哲学的思想框架，理解还原、意向性、时间意识等诸多现象学难题。本文将继续以之为线索，并通过与超越论—现象学还原相对比，来探讨胡塞尔《逻辑研究》中的向实然状态的还原，以期澄清它的确切意涵、其是否可能、是否必要。这也将深化对胡塞尔整个还原方法的范围问题的探究。

      接下来先笼统谈一下胡塞尔现象学哲学及他的还原方法，以期打开讨论的宏观视野。胡塞尔经历了数学和自然科学(尤其是物理学)发生革命性转变——比如物理学从牛顿的运动学范式转向爱因斯坦的运动学范式——的时代。②他的现象学哲学，从根本上讲，是在当时数学和自然科学背景下所作的延伸性和补充性的思考和检视。总体来讲，可以说，胡塞尔仍旧坚持着自笛卡尔以来的近代哲学的基本哲思方式，即通过对既有观念和知识进行批判性考察来澄清它们的形成机制及其基础。在我看来，这一批判性工作，对胡塞尔来讲——对笛卡尔也是如此——首先意味着区分可被怀疑的和绝对不可被怀疑的观念(或知识)。胡塞尔的整个还原方法，笼统地讲，就意味着从那些可被怀疑的观念暂且退回到或回溯到那些绝对不可被怀疑的观念之上。继而，在进一步的工作中，可以以后者为基础来为那些暂且可被怀疑的观念之合法性提供某种可能的根据和辩护。胡塞尔的现象学哲学正是运行在对全部知识和观念进行彻底怀疑和重新奠基的张力之中，或许可以更大胆地说，这一张力贯穿和激发着整个西方哲学的思想脉动。

      可见，就现象学的认识论或知识论来讲，“何者可被怀疑、何者不可被怀疑”这个问题处在开端位置。这一问题涉及认识活动的真假或认识对象的虚实。由此就有了标题对本文的总体定位：虚实之辨。第一节将通过论述数学中实数和虚数，以及物理学中实像和虚像、可感对象和超感对象之间的区分，来阐述自然科学中的虚实之分，并从现象学的认识论角度对其加以审视和评价。数学、物理学和现象学哲学对峙而交融的思想态势将为理解胡塞尔提供原本且适当的语境，因为如上所说，他的现象学哲学就是在当时的数学和自然科学发展背景下兴起的。第二节将在现象学认识论框架下追问“到底何为真实的、实然的(reell)”“区分虚实的标准是什么”等问题，并通过分析比对胡塞尔不同时期的文本，以及借助迪特·洛玛(Dieter Lohmar)教授的解读，来澄清向实然状态还原的准确意涵和所指。③尽管笔者同意洛玛紧贴《逻辑研究》第一版的具体语境对这一还原的确切意涵所作的解读，但笔者并不像他那样认为，这一还原既(原则上)可行，又必要。④本文第三节将论证，这一还原为何既不可行，又不必要，而且——对认识论批判和意识结构描述的工作来讲——是有害的。

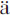      此外，在论述过程中，本文也将对“实然的”(reell)、“描述的”(beschreibend、deskriptiv)、“超越的(或超感的、超验的)”(transzendent)、“现象的”(phnomenal)、“现象学的”(ph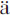nomenologisch)等概念作必要澄清。需要认识到，这些词不仅在现象学哲学中，而且在数学和物理学中都是常用词。在各学科交错关联中来反思和澄清这些基本概念，有着不可替代的意义和价值，对现象学这样一门(与成熟的数学或物理学相比)至今仍未成型的学科来讲尤为如此。⑤

      一、数学、物理学中的虚实之分及其认识论反思

      在日常德语中，reell有两个基本意思：(1)诚实的、正直的，如：诚实的人(ein reeller Mensch)；(2)现实的、真实的、实在的，如：现实的机遇(eine reelle Chance)。但在日常生活中，reell其实不是一个常用词，人们更会用ehrlich来表达“诚实”，更会用wirklich来表达“现实”。不过，在学术话语中，该词却是相当重要。

      数学中的实数，在德语的表达中，就是reelle Zahlen。与之相对的是虚数(imagin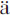re Zahlen)。⑥两者共同组成复数(即复合起来的数，komplexe Zahlen)，其表现形式为：z=a+bi(a，b为实数，i=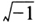为虚数基本单位)。⑦在此可以追问：实数和虚数的区别在哪里？实数的字面意思是真实的、现实的、实在的数。那实数在什么意义上是真实的、实然的，而虚数在什么意义上是虚假的、虚构的呢？

      从素朴的日常观点来看，实数的真实性在于它们与现实物理事物的对应。比如将自然数对应于现实物理对象的数量。⑧分数(如1/2)、无理数(如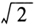)尽管并不对应数量，却对应于现实物的长度，比如，边长为l米的正方形井盖的对角线长度。⑨在这个意义上，我们可能认为，分数、无理数也与现实物相对应，因而具有真实性。但严格来讲，把实数的真实性归结为物理世界的现实性的做法是成问题的。只需指出一点：实数是严格连续的，任意两个实数之间，不论它们的数值多么接近，总还会有无限多个实数；而物理世界，在微观尺度上讲，是不连续的，原子间总有空隙。⑩这种不一致性决定了，不能把实数的真实性归结为其与物理事物的对应。