云南省图书馆机构用户,欢迎您!
美国博士生教育的发展历程对于推动我国高层次创新人才培养具有重要参考价值。基于博士生教育动力学模型揭示的链式反应规律,定量分析美国学术类博士学位授予数据与其指数模型的偏离程度,发现美国160多年来授予规模在遵循分段指数规律增长的总体趋势下,经历了8个约20年为周期的倒“U”型“增长—衰减”波动。其规律可近似为分段指数函数与周期函数的组合。提出基于该周期波动规律的授予规模定量预测方法,实测表明其预测优于美国国家教育统计中心基于多元线性回归模型的结果。给出2021-2030年美国学术类博士学位授予规模逐年预测,认为总体保持指数增长趋势,正在进入下行偏离通道、逐步衰减至谷底后将开启新的周期,2030年授予规模接近10万。
 S(t)为t年指导教师规模,A(t+1)、Q(t+1)、C(t+1)分别为t+1年招生、退出和学位授予规模。通过等式(1-6)可得指导教师、招生、退出和学位授予规模的表达式,由此可知这些博士生教育相关的主要规模数据均符合指数变化规律。其中学位授予规模为:
S(t)为t年指导教师规模,A(t+1)、Q(t+1)、C(t+1)分别为t+1年招生、退出和学位授予规模。通过等式(1-6)可得指导教师、招生、退出和学位授予规模的表达式,由此可知这些博士生教育相关的主要规模数据均符合指数变化规律。其中学位授予规模为:  在以时间为横轴、求取自然对数后的规模数据为纵轴的单自然对数坐标系中,其图形近似为具有不同斜率的折线段组合,可以通过分段线性拟合进行参数估计[13]。 2.博士生教育规模数据的偏离度 定义博士生教育规模数据的成长偏离度(以下简称“偏离度”),为实际规模数据与相应指数规律基线数据(目标数据)之差所占基线数据的比重。学位授予数据的偏离度为:
在以时间为横轴、求取自然对数后的规模数据为纵轴的单自然对数坐标系中,其图形近似为具有不同斜率的折线段组合,可以通过分段线性拟合进行参数估计[13]。 2.博士生教育规模数据的偏离度 定义博士生教育规模数据的成长偏离度(以下简称“偏离度”),为实际规模数据与相应指数规律基线数据(目标数据)之差所占基线数据的比重。学位授予数据的偏离度为:  其中
其中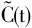 为学位授予实际数据,C(t)为学位授予基线数据,可由拟合所得分段指数函数计算。 对博士生教育实际规模数据取自然对数,基于等式(9)通过分段线性拟合进行参数估计。以分段指数函数作为基线函数,求取实际数据和基线数据之间的偏离度,进行偏离度分布分析,有助于进一步理解博士生教育的变化规律。这里以美国学术类博士学位授予数据为例进行讨论。 NCES传统统计口径①美国学术类博士授予数据②分段指数拟合和单自然对数坐标下分段线性拟合结果如图1。可分为形成阶段、工业化时代和信息化时代三个发展阶段,近100年来经历一战、二战、冷战前期、冷战后期和后冷战期等5个“U”型“衰减—恢复”周期[13]。 (1)偏离度的“增长”和“衰减”。基于图1数据,以分段指数函数计算结果作为基线数据,求得美国学术类博士学位授予数据偏离度曲线如图2上半部分虚线所示。
为学位授予实际数据,C(t)为学位授予基线数据,可由拟合所得分段指数函数计算。 对博士生教育实际规模数据取自然对数,基于等式(9)通过分段线性拟合进行参数估计。以分段指数函数作为基线函数,求取实际数据和基线数据之间的偏离度,进行偏离度分布分析,有助于进一步理解博士生教育的变化规律。这里以美国学术类博士学位授予数据为例进行讨论。 NCES传统统计口径①美国学术类博士授予数据②分段指数拟合和单自然对数坐标下分段线性拟合结果如图1。可分为形成阶段、工业化时代和信息化时代三个发展阶段,近100年来经历一战、二战、冷战前期、冷战后期和后冷战期等5个“U”型“衰减—恢复”周期[13]。 (1)偏离度的“增长”和“衰减”。基于图1数据,以分段指数函数计算结果作为基线数据,求得美国学术类博士学位授予数据偏离度曲线如图2上半部分虚线所示。