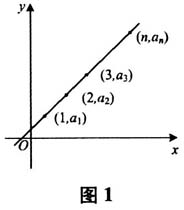
如果说学习数学的终极目标是用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界,那么,无论“数学眼光”远近与高低,还是“数学思维”的深浅与宽窄,其实都需用“数学语言”来表达,“让不可见变成可见”[1].数学语言对培养数学抽象与直观想象能力起到不可或缺的助推作用,反之,通过数学抽象与直观想象又不断锤炼数学语言,甚至说,人类语言的产生和发展就是源于抽象能力和直观想象能力的发展. 数学语言古已有之,源远流长,其过程始终离不开“数学抽象”和“直观想象”,虽然当时并没有这两个数学术语. 人们在原始生活中逐渐抽象出数字,在公元前500年左右,数学主要是有关数字的一种学问,即古巴比伦和古埃及时期的数学.因此,在这些远古文明中,数学绝大多数都是以算术为主的.从大约公元前500到公元前300年的这一时期,是古希腊数学的时代,那时的数学家主要研究几何学,最经典的就是欧几里得撰写于公元前350年的《几何原本》,在第一册中,欧几里得利用后来被称为欧氏几何的一个有关定义与设推(公理)系统,企图捕捉平面上规则图形如直线、多边形与圆形的抽象模式.在我国,有一道古代数学名题“鸡兔同笼”,后来通过代数抽象建立了简单的方程组,得出了普遍意义上这类数学问题的解决方法.南北朝时期杰出的数学家祖暅沿用刘徽的数学思想,展开丰富的直观想象和数学抽象,利用“牟合理论”进行体积计算,得出“幂势相同,则体不容异”的结论,现称“祖暅原理”. 本文主要就概念教学的过程中,数学语言在培养数学抽象与直观想象能力的表征与助推作用,谈谈自己的感想. 一、数学语言与数学抽象 数学语言可分为抽象性数学语言和直观性数学语言,包括数学概念、术语、符号、式子、图形等.数学语言又可归结为文字语言、符号语言、图形语言.抽象性不是数学特有的,数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程,主要包括:从图形与图形关系、数量与数量关系抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,从而用数学术语或符号等予以表征. 数列的概念本身是从实际生活中抽象出来的一列有序的数字.等差数列的概念是在数列的基础上进行强抽象所形成的一个特殊的数列模型.正如上面所说,用数学语言表征一个比较完整的概念一般会经历文字语言、符号语言和图形语言这3个不同的阶段,下面以等差数列的概念教学为例. 在实际生活中常常会遇到这样一些特殊数列: (1)某学校小剧场有40排座位,第一排有16个座位,从第二排起,后一排都比前一排多2个座位,那么各排的座位数依次是 16,18,20,22,24,26,….① (2)诺沃尔在1740年发现了一颗彗星,后来,人们推算这颗彗星将每隔83年出现一次,那么从发现那年算起,这颗彗星出现的年份依次为 1740,1823,1906,1989,2072,….② (3)第23届到第31届奥运会举行的年份依次为 1984,1988,1992,1996,2000,2004,2008,2012,2016.③ (4)某钢材库新到一批规格相同的圆钢,现把它们堆成三角形垛,由于受到地域的限制,假如最下面一层放26根,从第二层起,每一层比下面一层少放一根,则从下往上堆放的圆钢数为 26,25,24,23,….④ 上面这些数列有什么共同点?用文字语言可表述为:如果一个数列从第二项起,每一项减去它的前一项所得的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.

二、数学语言与直观想象 直观想象,即“几何直观和空间想象”.它是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.可以这么说,几何直观为空间想象提供了认识基础,空间想象为几何直观和由之向整体把握的发展提供了方法,是一嵌套循环的互动关系[2]. 显然,直观想象不仅限于立体几何的教学中.下面以导数概念的起始小节中“平均变化率”为例,彰显数学语言在培养直观想象能力与素养的表征作用. 2017年10月江苏省南通市教育局组织的正高级职称评审过程的课堂评议环节在南通市第三中学举行,笔者为突出该课题中的“变化”两字,即兴改编了白居易《大林寺桃花》诗一首,感受大自然季节的交替“变化”.

 二、数学语言与直观想象 直观想象,即“几何直观和空间想象”.它是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.可以这么说,几何直观为空间想象提供了认识基础,空间想象为几何直观和由之向整体把握的发展提供了方法,是一嵌套循环的互动关系[2]. 显然,直观想象不仅限于立体几何的教学中.下面以导数概念的起始小节中“平均变化率”为例,彰显数学语言在培养直观想象能力与素养的表征作用. 2017年10月江苏省南通市教育局组织的正高级职称评审过程的课堂评议环节在南通市第三中学举行,笔者为突出该课题中的“变化”两字,即兴改编了白居易《大林寺桃花》诗一首,感受大自然季节的交替“变化”.
二、数学语言与直观想象 直观想象,即“几何直观和空间想象”.它是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.可以这么说,几何直观为空间想象提供了认识基础,空间想象为几何直观和由之向整体把握的发展提供了方法,是一嵌套循环的互动关系[2]. 显然,直观想象不仅限于立体几何的教学中.下面以导数概念的起始小节中“平均变化率”为例,彰显数学语言在培养直观想象能力与素养的表征作用. 2017年10月江苏省南通市教育局组织的正高级职称评审过程的课堂评议环节在南通市第三中学举行,笔者为突出该课题中的“变化”两字,即兴改编了白居易《大林寺桃花》诗一首,感受大自然季节的交替“变化”.