中图分类号:F240 文献标识码:A 文章编号:1003-8477(2017)04-0163-09 随着我国“创新驱动”与“科教兴国”战略的深化实施,作为科技进步与社会发展重要引擎的高等教育受到了越来越多的关心与关注,其在人才培养、科学研究、社会服务等方面的职能也被寄予了更多、更高的期待。长期以来,我国高等教育将主要精力集中在提高教育质量方面,而对教育的投入产出效率没有给予足够的重视。[1](p49-55)事实上,我国高等教育不只存在质量内涵提升的现实要求,也存在资源使用效率不高和资源浪费现象。[2](p97-102)近年来,国家逐渐加大了对高等教育的投资力度,在高等教育投入保持相对增长的背景下,[3]中国高等教育投入产出是否有效?效率如何?中国高等教育效率的演化是否存在空间关联性?高等教育效率在空间上是呈现收敛还是发散的变化趋势?影响高等教育效率收敛性的因素有哪些?探讨并明晰以上问题对整体把握中国高等教育效率的演化特征,揭示中国高等教育效率的收敛机制,促进高等教育协调发展具有重要的理论价值与现实意义。 高等教育效率是从经济学中的“效率”概念派生而来,其内涵和外延相对比较宽泛,目前学术界还没有统一的概念。但从已有的研究成果来看,大多从内部效率和外部效率、经济效率和社会效率、投入与产出的比例关系等视角展开论述与研究。①出于研究的目的,本文高等教育效率是指高等教育的有效产出与高等教育的投入之比。单位教育投入的直接产出数量越多、质量越高,其效率就越高;反之,效率就越低。 目前,国内外学者对高校科研效率研究较多,②而对高等教育“全要素”效率的研究则相对匮乏,尤其是利用非参数前沿法对高等教育效率进行研究的成果自20世纪90年代后才相继出现。代表性的研究成果有麦克米伦和丹特(McMillan & Data,1998)对加拿大大学的效率问题进行了研究;[4](p97-114)安伯特(Abbott,2003)对美国和澳大利亚大学的效率进行了研究;[5](p89-97)陈通等(2002)利用数据包络分析DEA(Data Envelopment Analysis,DEA)对我国高等教育投入产出的相对有效性进行了分析与评价;[6](p13-16)任保奎等(2008)对北京高等教育效率与上海、江苏、浙江等9个省市进行了比较研究;[7](p77-80)徐健等(2009)运用DEA模型对我国31个省区市的高等教育效率进行了综合评价,并对10个高等教育大省中无效率的省份进行了投影分析;[8](p81-85)李祥云等(2011)通过构建数据包络分析及其二次相对效率模型,估算了部分教育部直属高校投入产出的技术效率和管理效率;[9]魏梅(2012)运用动态方向性距离函数对1995-2009年中国高等教育效率进行了核算,并从空间外溢的视角考虑了影响区域高等教育效率增长的因素;[2](p97-102)石丽等(2015)运用超效率DEA模型分析了中国高等教育效率的空间差异及演化特征,并建立空间计量模型回归分析全要素生产率各分解指标对高等教育效率的影响;[10](p21-26)夏焰、崔玉平(2015)运用全要素生产率指数和空间统计分析方法,从时间和空间两个维度研究了我国省域高等教育效率及其空间交互特征。[11](p29-34)在高等教育效率分析的基础上,个别学者进一步探讨了我国高等教育效率的收敛性问题。韩海彬等(2010)采用Malmquist指数法对1999-2006年中国高等教育生产率的变动情况进行了分析,并对中国高等教育技术效率的绝对收敛性进行了检验;[12](p58-62)沈能等(2014)运用Bernard时间序列收敛模型对我国大学知识创新效率的空间趋同性进行了检验。[13](p21-30) 现有的研究成果对我国高等教育效率及收敛性问题进行了积极的探索并得出了许多有益结论,这为本研究的开展提供了宝贵的借鉴。通过对以上文献的回顾梳理可以发现,现有对我国高等教育效率及其收敛性的研究仍有以下几个方面可以改进:首先,非参数径向DEA虽然保证了效率测度边界的凸性,但同时带来了各决策单元投入产出要素的“松弛”问题,使得效率值测算相对偏高。本研究所采用的SBM(Slack Bsaed Measure,SBM)模型能够有效改进这一点;其次,大多数研究选取的投入产出指标并不十分完善,且研究时间跨度相对较短,本文则利用1999年高等教育扩招以来连续15年的数据进行测算,以期测量出更加精准的中国高等教育效率及其发展趋势;第三,大多数研究并未涉及中国高等教育效率的收敛性问题,更未考虑其空间相关性和空间效应,本研究采用空间面板计量模型可有效解决传统模型可能出现的偏误。 二、我国高等教育效率的测算与分析 (一)SBM模型 数据包络分析(DEA)是一种基于被评价对象间相对比较的非参数技术效率分析方法,是由美国的查恩斯(Charnes)、库珀(Cooper)和罗兹(Rhodes)三人于1978年首次提出。[14](p429-444)它通过计算所有决策单元实际生产点与生产前沿面的距离来确定其效率测度。DEA保证了效率测度边界凸性,但对各决策单元松弛改进的部分在效率值的测量中并未得到体现。[15]出于这样的考虑,托恩(Tone,2001)提出了非径向SBM模型,该模型直接利用投入产出松弛构建模型的目标函数,适用于多投入多产出的复杂生产系统的分析。[16](p498-509)该模型如下:

其中m表示投入要素的种类;n为产出的种类;

分别表示投入、产出、投入松弛、产出松弛;
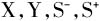
为决策单元对应的矩阵;λ是一组列向量,代表各决策单元的权重;θ为决策单元的效率得分。
 其中m表示投入要素的种类;n为产出的种类;
其中m表示投入要素的种类;n为产出的种类; 分别表示投入、产出、投入松弛、产出松弛;
分别表示投入、产出、投入松弛、产出松弛;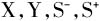 为决策单元对应的矩阵;λ是一组列向量,代表各决策单元的权重;θ为决策单元的效率得分。
为决策单元对应的矩阵;λ是一组列向量,代表各决策单元的权重;θ为决策单元的效率得分。