高考招生制度改革的路径：竞争和配额的折衷

      我国现行高考招生制度是一种“配额制”。每省分得若干招生名额，由该省户籍考生竞争，考生不能“越界”占用别省名额。各省内部录取基本由考生成绩高低决定，即“高分高就，低分低就”，是一种“竞争制”。

      高考招生名额分配不均，导致各地高考成绩的分布模式明显不同。以北京和山东为例，若考生能力属于正态分布，则北京高考成绩更接近正态分布，而山东高考成绩明显向高分段集中，反映出考生努力竞争求胜的态势(图1)。实际上，相比其他省级地区(如最典型的山东和河南)，京、沪考生考取大学的机会大得多，特别是考取本地一流大学的机会(表1)。

      “配额制”造成人均配额贫乏省份的考生难以考上好大学，即使成绩较好；而人均配额充裕省份的考生较易考上好大学，即使成绩不那么出色。①从全国考生和大学的匹配看，“高分低就”型匹配中的考生和“低分高就”型匹配中的大学都是不满意的，两者有积极性放弃已有匹配对象寻求新匹配。匹配理论指出，“配额制”的高考招生结果是“不稳定”的。

      “配额制”不稳定的高招结果，第一，挫伤了考生“生产性努力”，激发其“分配性努力”。对招生名额贫乏地区的某些考生，努力读书、在本地考高分并非最优选择，“高考移民”甚至改换国籍避开高考等才是最优。第二，降低了高等教育选材效率，降低了人力资本积累预期水平。一般地，“高分高就，低分低就”的安排使人才培养效益最大，反之培养效益受损：次级大学可能耽误优等生，次级生可能浪费优等大学教育资源。②第三，扭曲了未来工作机会的分配，导致宏观产出和人力资本积累的损失。文凭可视为劳动力向企业发送的一种能力信号，“配额制”录取的不公平可能使高能力者发送低能力信号，而低能力者发送高能力信号，导致工作机会分配不公平。考虑到“干中学”，人力资本积累也受损。第四，高招“配额制”(含配套的户籍地高考制度)还有间接不利影响。改革以来，我国经济发展离不开大规模劳动力转移和城市化，这也是建立现代国家、向现代市场经济迈进的重要步骤，这就要求一个能打通各地隔阂、在全国范围内有效配置资源的规则。高招“配额制”却违背了该要求。

      

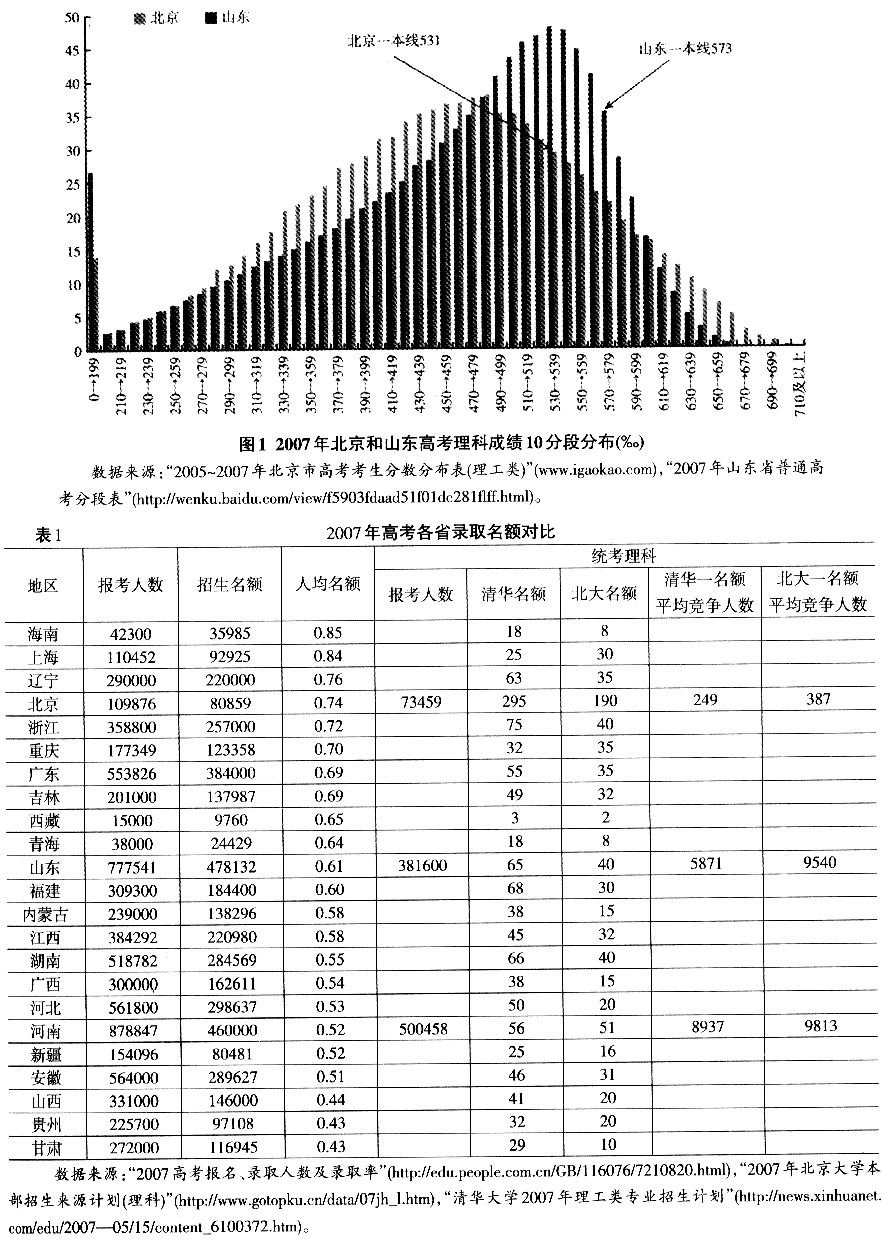      高招“配额制”须改革，但亦须顾及既得利益。地方政府和居民为当地大学持续投入人力、物力和财力，根据“谁投资，谁受益”，既得利益应得到承认。因此，稳定性和既得利益是高招制度改革应兼顾的目标。但二者不能兼得：若将高招制度推向竞争制以实现匹配稳定，则人均配额较多的省份的考生既得利益严重受损；若维持现行配额制，则人均配额较少的省份的考生将承受巨大的不公平。可取、可行的高招制度不应是极端配额制或竞争制，而应介于二者之间。

      本文提出四种典型折衷制度：人口比例配额制、出资比例配额制、次级配额制和异地高考配额制。通过数值模拟，分析比较了全部六种制度的(分地区)录取结果、偏离竞争制匹配的情况和使配额制中既得利益受损(因而引发反对)的情况，得出次级配额制最可取的结论。本文分析还表明，当前呼声很高的“异地高考”，并非改革现行高招制最可取的方案，因为“异地高考”仍属于配额制，并在偏离稳定匹配和损害既得利益两方面都差于竞争制。

      Azevedo & Leshno(2011)以大学招生为例，研究双边匹配市场中一边代理人(有限个大学)被匹配给另一边大批代理人(学生的连续统)的问题，他们提出Gale & Shapley(1962)大学招生模型的一个变体，得到四个重要结论：一般地，(1)该连续统经济存在唯一稳定匹配；(2)该稳定匹配随经济参数变化而连续变化；(3)用大的离散经济(数量大但有限的学生)序列逼近该连续统经济，相应的稳定匹配序列收敛到该连续统经济的唯一稳定匹配；(4)该连续统经济唯一的稳定匹配由“市场出清分数线”方法获得。对本文的高招经济，结论(1)保证了稳定录取结果的存在性和唯一性，结论(3)保证了现实离散经济的数值模拟录取结果的收敛性和稳定性，结论(4)保证了本文的“批次录取”方法所得录取结果的稳定性。③

      Gale & Shapley(1962)提出了“延迟录取”(deferred acceptance)程序，用以在大学招生问题中获得“稳定”和“申请人最优”的学生-学校匹配结果。该程序步骤如下：第1轮，所有学生向自己最喜欢的一所学校提交申请，所有学校按自己的招生名额将其评价靠前的学生申请列在待录取名单上，但并不录取他们，并拒绝其他申请。第2轮，所有上一轮被拒绝学生向自己第二喜欢的学校提交申请，所有学校按自己的名额留下这一轮收到的和其上一轮待录取名单上的所有学生申请中评价靠前的，形成新的待录取名单，并拒绝其他申请……第n轮，当每一个学生都列在某一大学的待录取名单或已被所有大学拒绝，录取程序结束。所有大学待录取名单上的所有学生被正式录取，被所有大学拒绝的学生落榜。

      聂海峰(2007)分析了高考招生中考后知分志愿填报博弈。完全信息时，这个显示偏好博弈虽有唯一纳什均衡且该均衡是帕累托有效和公平的，但对于大学真实的偏好并非每个考生的均衡策略。达到均衡结果需要参与人之间的协调，而协调成本相当高，且若协调失灵，会出现高分低就甚至高分落榜情况。解决此问题的一种方法是使用Gale-Shapley的“延迟录取”程序。此时真实偏好是学生的优势策略，由此达到的录取结果也是帕累托有效和公平的。