多重因素分析在大学评估指标整合中的应用

      中图分类号：G640 文献标识号：A 文章编号：2095－1760(2013)01－0042－12

      一、引言

      对大学进行评估，主要是对大学办学水平，包括教育质量和办学方向进行综合评价。通过评估完善现代大学制度，提升大学的科研实力，以学科评估培育优势学科和优化学术队伍，以绩效评估激励大学之间的公平竞争和促进特色办学，以社会评估促进政府管理职能转变，等等。[1]从课程评估、学科评估到绩效评估和社会评估，可见教育评估的形式是多元化的，其宗旨和功能亦具有多样性。然而要充分发挥教育评估与评价的作用，一方面需要根据评价目标构建合理的评价指标体系[2]，另一方面则需要能将各种评估指标加以有效整合的统计方法的支撑[3]。

      多重因素分析(Multiple Factor Analysis,MFA)是基于主成分分析(Principal Components Analysis,PCA)的一种统计方法，与传统的因素分析不同，传统的因素分析方法是将所有变量作为一个整体来进行因子提取，用较少的因子来表征数据的特征。当所收集的数据既有连续变量又有分类变量或是明显属于不同维度的数据时就不适宜采用传统的因素分析方法。多重因素分析通过将变量分成几个子群，对每个子群和总群分别进行主成分分析，进而考察子群与总群之间和各个子群之间的关系，为深入了解事物(变量)之间的关系提供了一种有效的数据分析方法，鉴于多重因素分析方法能够同时处理具有不同属性的变量，它就成为同时分析(simultaneous analysis)或联合分析(joint analysis)的重要方法之一。[4][5]

      本文将着重介绍多重因素分析方法的原理，并通过实例来说明多重因素分析的应用，希望能够丰富教育评估与评价的数据分析手段，进而拓展教育评价等相关领域的研究空间。

      二、多重因素分析方法的原理

      多重因素分析方法特别适合于对一批观测对象测量了许多指标的情况。由于不同的变量其测量空间或数据域不同，简单地将所有变量合在一起进行分析，正如非标准化的主成分分析会导致具有较大变异的变量组群对统计结果具有决定性作用一样[6]，对所有变量进行整体分析的愿望则无法达成。而在样本量较少时，传统的因素分析方法又会面临样本适当性问题。尽管高尔(Gower)提出采用高尔系数将所有变量转换至［0，1］区间来解决非标准化问题[7]，但包括随后对高尔系数的改进[8]，针对的都是单独的变量。主成分分析中变量标准化的过程相当于将不同的变量赋予不同的权重后再进行分析。而当变量属于不同组群，需要将一个组群的所有变量作为一个整体(或同时)来考虑，其关键在于找到能够反映各个变量组群变异度的权重系数(相当于主成分分析中的标准差)。这正是多重因素分析方法有效地将隶属于不同组群的变量整合在一起的核心思想所在。

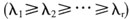      多重因素分析中，当一个变量组群在某个方向上具有较大惯量时，最终该变量组群会对整体分析的主轴产生影响偏差，因此需要对每个变量组群的最大轴惯量进行归一化处理。即每个变量组群的变量先各自进行标准化和归一化处理，再对所构成的矩阵进行奇异值分解，将奇异值作为矩阵的标准差，然后利用首奇异值对各变量值实施加权处理，从而使最大轴惯量归一化。由于奇异值的平方等于对该变量组群进行主成分分析后所得的特征值，所以在计算奇异值时也通常利用主成分分析计算每个变量组群的特征值，借此对每个变量组群进行加权，最后将加权后的变量组群拼接在一起通过主成分分析或矩阵的奇异值分解来进行整体分析(参见图1)。通过整体分析除能够揭示由观测对象所组成的空间结构外，多重因素分析还提供了叠加表征方法，既可以将变量叠加至空间中，也可以将观测对象叠加到空间中，以图形化的方式来直观揭示观测对象之间、变量之间、组群之间或因素之间的关系。针对不同变量组群对观测对象所进行的主成分分析(因素分析)可以称之为“局部分析”，那么通过局部分析所得到的观测对象的空间结构之间是否具有相似性？它们之间的关系如何？这正是引言中所涉及的问题。

      

      图1 多重因素分析结构示意图

      图2中，全局空间可被视作所有局部空间的集合，通过将局部空间中的观测对象投射到全局空间的主轴上就能够直观地比较对象之间的关系。当观测对象在不同变量组群上具有相似空间结构时，映射点会彼此靠近。通过投射还可以考察观测对象在局部空间与全局空间的表征点之间的距离。类似地，还可以考察和比较变量组群(指标)之间的关系、组群内的变量与所属组群间的关系。当变量组群具有相似空间结构时(观测对象之间的距离在不同的局部空间具有相似性)，且局部空间与全局空间的距离越近，表明某变量组群与整体结构在某个映射轴上的相似性越高。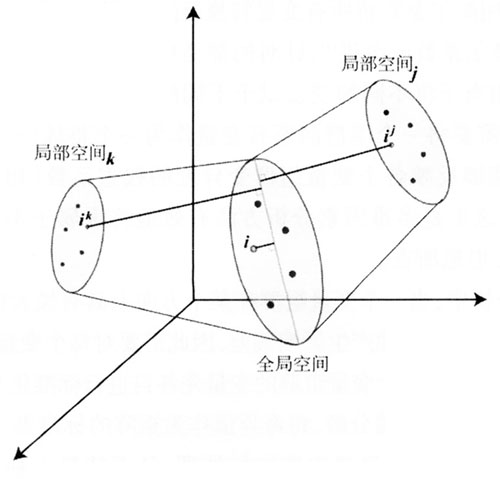

      

      图2 局部空间在全局空间中的映射关系

      注：i为某观测对象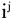；表示观测对象i在变量组群j所构成的空间中的表征。