区域高等教育对经济增长贡献率差异的内部因素分析

      中图分类号：F08：G40-054文献标识码：A文章编号：1672-8106(2012)02-0095-08

      一、引言

      高等教育作为人力资本投资的重要渠道，日益引起人们的重视。关于高等教育对经济增长贡献研究的文献虽已不少，但现有研究大多集中在高等教育对经济增长贡献率的估算上，有关区域高等教育①对经济增长贡献率差异因素的深入研究尚未多见，而且在估算方法上往往忽略了不同层次教育之间在质量上的差别，以及我国不同区域之间在经济社会发展方面的特殊性。

      本研究以各级普通学校生均教育经费支出作为衡量人力资本投入质量指标，以就业人员中受各级教育程度劳动者人数作为衡量人力资本投入数量指标，既考虑到了人力资本投入的数量因素，又考虑到了人力资本投入的质量因素；以物质资本存量作为物质资本的投入指标；以GDP作为经济的产出指标。根据上述指标重新构建C-D生产函数，利用面板数据估算出1996-2007年间我国东、中、西、东北四大区域②的人力资本产出弹性系数，据此计算出各地区高等教育所形成的人力资本在此期间对经济增长的贡献率，并对影响区域高等教育经济贡献差异的内部性因素进行了深入分析。

      二、区域高等教育对经济增长贡献率的估算

      为估算区域高等教育对经济增长的贡献率，需要利用包含人力资本的两部门C-D经济增长模型计算出教育所形成的人力资本的产出弹性系数。其形式为

      Y=AF(K，H)(1)

      式中，Y代表产出GDP③；K代表物质资本存量④；H代表人力资本存量⑤。

      

      由于这些制度性的控制变量都是百分比的形式，因而，采用指数回归模型来确定回归模型中的解释变量和被解释变量之间的关系。由此可得如下回归模型

      

      估算区域高等教育对经济增长的贡献率，既要考虑到区域高等教育自身的差异(体现在截面单元上)，又要考虑到国家政策的影响(体现在时间序列上)，本研究中使用能够同时反映研究对象在截面和时间单元两个方向上变化规律的Panel data面板数据，先将全国31个省级行政区划分为东、中、西、东北四大区域，在估算出各大区域教育所形成人力资本的产出弹性系数基础上，进一步计算出各个省级行政区高等教育对经济增长的贡献率。在使用面板数据模型时，首先要进行模型的设定检验以确定使用哪种形式的面板数据模型。

      考虑到截面样本之间存在异质性，本文使用似不相关回归(Seemingly Unrelated Regression，SUR)进行检验，对模型进行相应的广义最小二乘法(Generalized Least Squared，GLS)估计。SUR是考虑到方程间的误差项存在异方差和同期相关的条件下，估计多个方程所构成的系统参数。在使用SUR进行检验时，面板数据方程估计权重选用两种：截面成员残差协方差矩阵和时期残差协方差矩阵。其中，前者要求时期个数必须大于截面成员个数，后者则相反。本文样本中四个地区的截面成员分别为10、6、11、3，时间期数为12，因此，在实证中使用GLS回归，面板数据方程估计权重都使用截面成员残差协方差矩阵。计量结果如表1所示。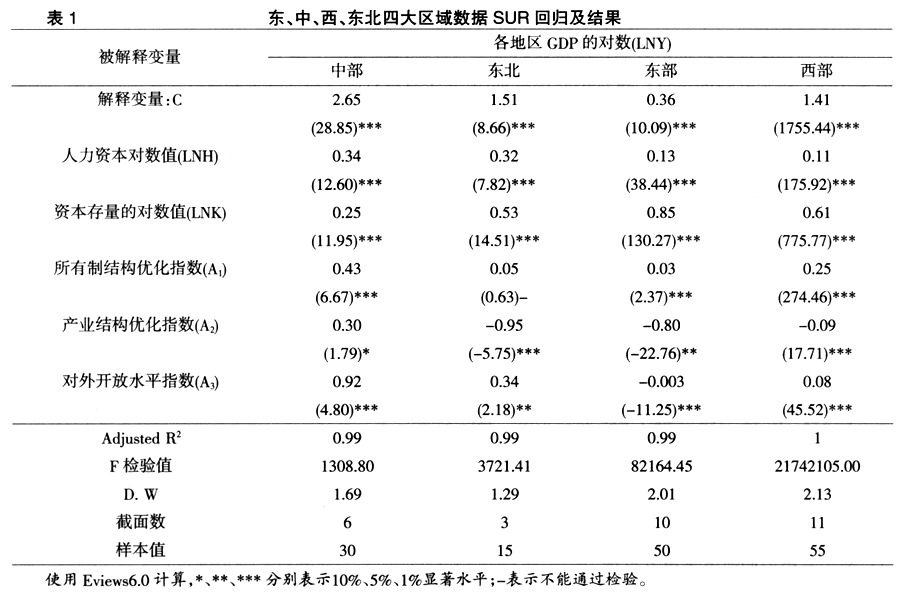

      

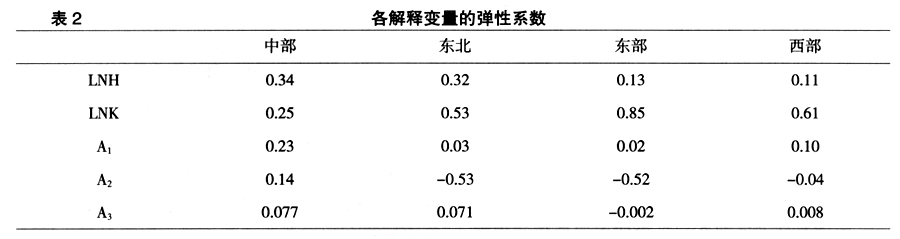
      回归方程具有较高的拟合优度，F统计量较大，表明方程顺利通过显著性检验，方程的D.W统计量接近2表明模型不存在明显的序列相关问题。此外模型回归过程中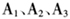使用的是百分比形式，其弹性系数需要通过对如下公式进行相应的调整后计算出来。各解释变量弹性系数的计算结果见表2。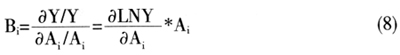

      

      

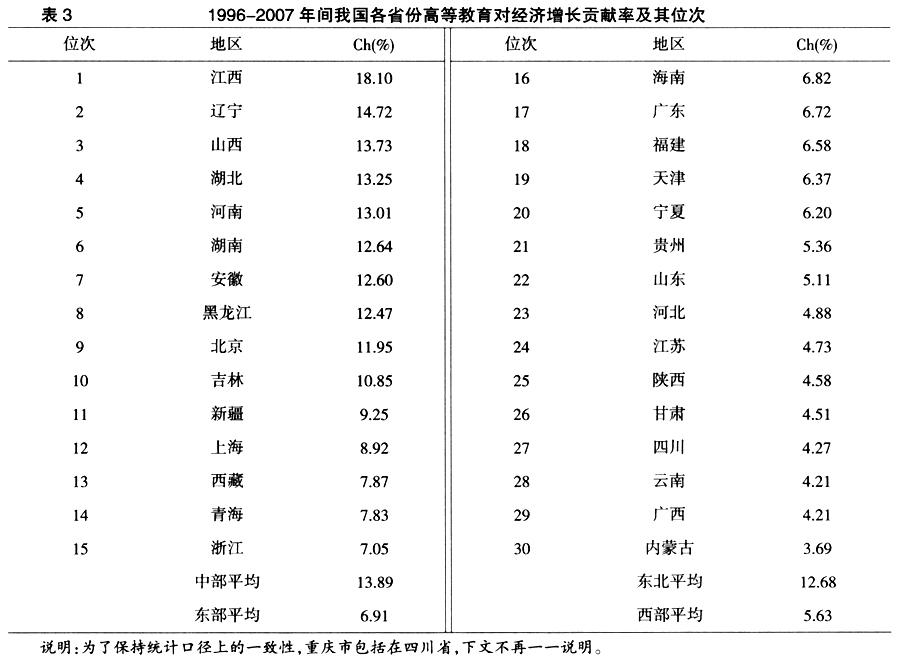
      从表3可以看出，1996-2007年间我国区域高等教育对经济增长贡献率，不同区域之间，以及同一区域不同地区之间存在较大的差异。四大区域之间自中部、东北、东部、西部呈梯次递减的趋势；不同地区之间的差距更为明显，区域高等教育对经济增长贡献率最高的省份是中部经济欠发达的江西省(18.10%)，最低地区是西部经济欠发达的内蒙古(3.69%)，前者是后者的约5倍。