云南省图书馆机构用户,欢迎您!
目前,我国各级各类教育发展战略目标的确定尤其是2020年高等教育毛入学率达到40%的目标是缺乏科学依据的。根据科学、技术和社会生产计量分析的基础之上建立教育发展的数学模型以及教育发展的系统分析,可以得出:与十六大提出的2020年人均国内生产总值比2000年翻两番的奋斗目标相适应,高等教育毛入学率应达到50%,实现高等教育的普及化。
 依据现代经济理论,社会经济增长由科技进步投入、物质资本投入和劳动力投入共同作用,其计量公式为:
依据现代经济理论,社会经济增长由科技进步投入、物质资本投入和劳动力投入共同作用,其计量公式为: 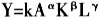 其中,k、α、β、γ为常数,Y为经济增长,A为科技进步投入,K为固定资本投入,L为劳动力投入。 这个公式在总体经济分析中使用是最广泛的,因为,它能够全面描述和解释生产过程中投入要素科技、人力资本、物质资本与产出之间的关系,符合经济理论分析及观测到的经济现象。另外,此函数是以时点序列统计的函数,对经济增长的解释能力较强。在以上公式中,劳动力投入包括劳动力数量和质量增长。舒尔茨的经济余数教育收益率法和丹尼森的因素分析法都是依据这种理论计量教育收益的。 2.劳动力教育质量水平的计量分析 在整个社会生产的投入要素中,人力、资本及技术进步都是随着时间的变化而变化,将其作为时间的函数分别记为: L=L(t),K=K(t),A=A(t) Y=Y(A,K,L) 对于生产函数在任意时刻,P(A,K,L)=0的等产量面上的方向导数为:
其中,k、α、β、γ为常数,Y为经济增长,A为科技进步投入,K为固定资本投入,L为劳动力投入。 这个公式在总体经济分析中使用是最广泛的,因为,它能够全面描述和解释生产过程中投入要素科技、人力资本、物质资本与产出之间的关系,符合经济理论分析及观测到的经济现象。另外,此函数是以时点序列统计的函数,对经济增长的解释能力较强。在以上公式中,劳动力投入包括劳动力数量和质量增长。舒尔茨的经济余数教育收益率法和丹尼森的因素分析法都是依据这种理论计量教育收益的。 2.劳动力教育质量水平的计量分析 在整个社会生产的投入要素中,人力、资本及技术进步都是随着时间的变化而变化,将其作为时间的函数分别记为: L=L(t),K=K(t),A=A(t) Y=Y(A,K,L) 对于生产函数在任意时刻,P(A,K,L)=0的等产量面上的方向导数为:  这说明,技术进步,人力、资本变化的比例不同,经济生产的效果不同。更进一步地说就是:一个国家或地区投入在科技进步、劳动力及资本的分配策略不同,所得到的经济增长幅度也就不同。 根据梯度最大值原理,当F1×F2=0时,Y增长最大。
这说明,技术进步,人力、资本变化的比例不同,经济生产的效果不同。更进一步地说就是:一个国家或地区投入在科技进步、劳动力及资本的分配策略不同,所得到的经济增长幅度也就不同。 根据梯度最大值原理,当F1×F2=0时,Y增长最大。 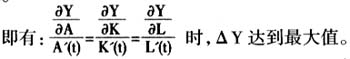 这说明,保持经济的高速增长,尤其是在人均劳动资本的高速增长的情况下,劳动力质量的水平与科技进步应是均衡发展,增长变化的幅度应是相等的。当人力资本即劳动力教育水平和物质资本的科技进步的增长率通过系统运行所产生的边际效率相同或比较接近时,投资的效益才能达到最大值。
这说明,保持经济的高速增长,尤其是在人均劳动资本的高速增长的情况下,劳动力质量的水平与科技进步应是均衡发展,增长变化的幅度应是相等的。当人力资本即劳动力教育水平和物质资本的科技进步的增长率通过系统运行所产生的边际效率相同或比较接近时,投资的效益才能达到最大值。 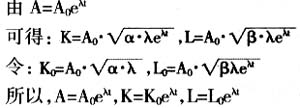
 分别对劳动力数,劳动力每人完成的学年数和劳动力完成的总学年数对数作回归分析,只有劳动力每人完成的学年数在统计上显著,有:
分别对劳动力数,劳动力每人完成的学年数和劳动力完成的总学年数对数作回归分析,只有劳动力每人完成的学年数在统计上显著,有:  把劳动力总数、劳动力每人完成的学年数及完成总学年数每10年的净增长率用图形表示出来,呈现出不同的增长形态,与1920年至1957年美国经济全面大发展相关程度高的是劳动力每人完成的学年数。这同时说明,适应科学、技术的现代化发展,在人力资本投入中侧重的是劳动力质量而非数量,经济增长越来越依赖于劳动者的素质提高,越来越需要教育提供人的知识、智力和综合素质支撑。 3.教育发展计量的数学模型 在科学技术的作用下,人类生产能力的提高和与其相适应的劳动力教育水平的提高都是时间的指数函数,具有指数函数性质,用公式表示为:
把劳动力总数、劳动力每人完成的学年数及完成总学年数每10年的净增长率用图形表示出来,呈现出不同的增长形态,与1920年至1957年美国经济全面大发展相关程度高的是劳动力每人完成的学年数。这同时说明,适应科学、技术的现代化发展,在人力资本投入中侧重的是劳动力质量而非数量,经济增长越来越依赖于劳动者的素质提高,越来越需要教育提供人的知识、智力和综合素质支撑。 3.教育发展计量的数学模型 在科学技术的作用下,人类生产能力的提高和与其相适应的劳动力教育水平的提高都是时间的指数函数,具有指数函数性质,用公式表示为: