中图分类号：G643 文献标识码：A 文章编号：1001-4519(2006)06-0042-07 一、问题的提出 自80年代以来，我国研究生教育面临着经费不足的问题。特别是从1999年以来，研究生招生规模以高比例增长，在校研究生人数急剧扩大。①研究生教育规模的增长速度远大于我国人均GDP增长速度，大于公共教育经费、科研经费的增长速度。规模的快速扩张与投入的增长速度缓慢，无疑加重了研究生教育经费的供需矛盾。根据有关研究估算，目前国家拨付研究生教育经费只能覆盖实际在校研究生培养费用的50%左右，经费紧张的状况相当严重。在国家财政性高等教育经费拨款的幅度和比例不可能再有大的提高的背景下，合理配置教育资源，向有限的教育资源要效益已成为研究生教育发展的关键问题之一。 高校作为研究生培养的重要机构，只有提高办学效益，充分利用有限的人力、物力、财力资源，才能在经费短缺的情况下有效地提高教学质量，培养出更多更好的人才。规模效益是办学效益的重要方面，办学规模过小，成本高且不利于学生质量的提高，规模过大不便管理、工作效率低。在合理的幅度内，扩大办学规模可以降低生均教育成本，充分利用校内资源，形成规模效益。本文试就研究生教育的规模经济问题进行研究，从高等院校的研究生规模与成本之间关系的角度分析高校办学效益。 二、文献综述及理论框架的分析 最早提出规模经济问题的是英国人马克西和西尔伯斯通②，在他们合著的《汽车工业》一书中通过对汽车工业生产线的长期平均费用的研究，绘制出了著名的“马克西—西尔伯斯通曲线”。规模经济的核心涵义指在产出的某一范围内，平均成本随着产出的增加而递减的现象。③ 在高等教育领域，国内外学者做了大量实证研究，证实高等学校也存在规模经济。卡内基委员会 1972年的研究表明，全日制在校生规模在3,000-4,999人的私立研究性大学的生均教学成本，比相应规模在7,000-9,999人的同类院校要高25%。但非常小的院校和那些在校生人数在10,000-15,000人的私立院校都具有最高的成本。④斯图曼1985年所做的关于美国赠地学院（多数是研究性大学）的研究表明，在控制了专业数目、研究生比例和研究经费比例后，学校规模约在22,850名全日制在校生的院校比那些规模小约四分之一的院校生均经费要低21%左右。⑤柯恩等1989年对美国121个公立和私立大学（大部分是研究型大学）进行了规模效益的研究，结果发现，最有效率的学校是全日制在校生当量接近3万，并且获得的研究经费大约在8千万到1亿美元（1981-1982年的水平）的那些学校。⑥美国学者应用1979年123个发展中国家和23个发达国家数据分析后发现，当高等学校学生规模达到500人后，学生数增加和单位成本呈负相关关系，这在500-1000人范围内尤为明显，但学生规模达到10,000人后，单位成本不再下降。⑦对国内高校规模效益的研究起于1986年。1986年世界银行专家对我国136所曾经得到过世行贷款援助的高校进行了有关规模经济的实证分析，得出的结论是，在这些学校中存在着显著的规模经济。在达到8,000-10,000学生数之前，生均经常性成本随在校生的增加而有明显的减少；在达到8,000-10,000的规模后，生均经常性成本则基本保持不变。⑧之后，闵维方在80年代后期对中国136所高等学校数据分析也得到类似结果，就中国高等学校目前的环境和管理而言，临界规模约在 6,000人左右。上海市智力开发研究所应用1994年841所普通本专科学校（不包括特殊的艺术、体育院校）数据分析后获得了进一步发现，本科院校折合全时制在校生的临界规模在11,000人左右，专科院校在9,500人左右，用全日制本专科计算，分别为8,000人和7,500人左右。⑨最近对教育规模经济的研究已深入到高校内部系和专业规模，发现系和专业也存在明显的规模效益。 研究生教育作为高校人才培养的重要一部分，是否也存在规模效益？是否也存在适度规模？目前文献检索还没有相关实证研究。理论上，薛天祥阐述了探寻研究生教育适度规模的重要性和可行性。⑩他指出，在我国国力欠强、教育投资还很有限的条件下，探寻研究生教育的适度规模，有效地提高教育资源的利用率，充分发挥教育资源的效用效率，增强研究生教育办学的市场竞争力，显得格外重要和迫切。合理的学校研究生规模，有利于充分发挥教师和行政人员的职能潜力，提高校舍和基地使用面积的占有率，提高图书及实验设备尤其是大型精密仪器的利用率；也有利于物质技术装备的协同共用，增加新的边缘学科和专业，促进学校内外的联合协作。本文正是基于上述研究现状，实证分析规模与成本的关系。 高校的规模效益的源泉也得到了很好的解释：固定成本构成了规模经济的重要来源。在短期内，高校教育成本可以分为固定成本与可变成本。固定成本指在一定时间和一定学生数量的范围内，总成本中基本不受学生数量增减影响而相对固定的那部分费用，包括教育占用固定资产（如校舍、教学仪器设备、图书资料）及其折旧费和修理费；维修和管理人员的工资；编制内教师的基本工资；办公费、水电费、差旅费等。可变成本是指教育总成本中随着学生数量增减而变动的那部分费用，包括教职工的超课时报酬、奖金、临时聘用教职工工资；用于教学用的教材、纸张、文具以及其他学习材料；实验的耗费品等。正是由于校舍、教学仪器设备等固定资产在短期内具有“整体性”和“不可分”的自然属性，因此在一定范围内，高校可扩大其规模，增加其产出（学生人数），其成本不会成比例上升，固定成本随着产出的增加而分担，教育平均成本下降。从图1可以清楚地看出教育成本的变化情况。总成本TC随着学生人数Q的增加是逐渐递增的，固定成本FC在一定规模范围内不变，可变成本VC随着人数的增加呈递增趋势。当在校生的数量在Q[,1]点和Q[,2]之间时，高校现有的培养能力与学生所需的条件相当，固定成本不变，而单位可变成本VC/Q随着学生数量Q的增加而逐渐减小，这时平均成本递减，出现了规模经济。因此在保证教育质量的前提下，可通过利用现有资源来扩大教育规模和提高教育资源利用效率。
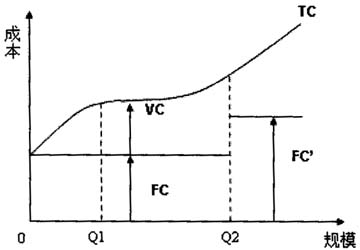
图1 规模与成本的关系 对教育规模效益进行探讨，由于方法和数据上的问题，一般是通过横断面数据散点图来直观地分析其成本变动趋势，并通过把某个学生平均单位成本与某种规模量度（如入学人数），以及其他控制变量（包括教育质量，例如用生师比来做代表）联系起来进行估算的，建立成本函数模型。通常说来，长期平均成本曲线有两种类型，分别为U型和L型。依据U型拟合函数通常是二次型，这种函数形式有唯一的最佳规模；依据L型拟合的函数通常是双曲线形式，这种形式不能获得最佳规模的估计，而只能近似地求解某个适度规模。参考前人研究成果与本研究的拟合优度，本文选用的是双曲线形式。考虑到数据的可获得性，我们主要以中国教育部直属的72所院校为依据展开分析。
