我国区域高等教育竞争力的实证研究

      中图分类号：G 640文献标识码：A文章编号：1004-8154(2006)05-0056-05

      一、引言

      已经有学者就区域教育竞争力与区域经济竞争力之间的相互关系进行了研究，证明二者之间的相关性达到0.81，并且区域教育竞争力是区域经济竞争力的先导因子[1]。区域综合实力的竞争归根结底是教育的竞争和高级人才的竞争，因此研究高等教育竞争力也是很有现实意义和必要性的。区域高等教育竞争力反映的是一地区高等教育在质量和规模两方面的综合水平和实力，它是区域竞争力的一个重要组成部分。

      目前国内已经有很多学者对教育竞争力作了多方面的研究和探讨，有的学者对教育竞争力和国家竞争力之间的关系进行了相关研究，认为国家竞争力的核心是人才的竞争，而人才的竞争归根结底是教育的竞争，因此国家竞争力的核心是教育竞争力[2] [3]；还有的学者从定性的角度对我国高等教育的国际竞争力进行多角度的分析，认为应该加速高等教育向经济中心转移，通过提高高等教育的国际竞争力来提升我国的国际竞争力[4] [5]；还有的学者对我国的区域教育竞争力运用实证分析的方法，对我国教育竞争力进行统计分析，把我国的教育竞争力按照由强到弱排列进行区域划分[6] [7] (P.1-6)。从以上这些已有的研究上来看，目前国内还没有学者专门针对我国的高等教育竞争力运用实证分析的方法进行区域划分。因此，本文在吴玉鸣等发表在2002年第3期《教育与经济》“我国区域教育竞争力的实证研究”(以下简称“吴文”)一文的基础上，对我国的高等教育竞争力运用主成分分析、因子分析和聚类分析的方法进行一次区域划分的尝试。

      二、实证分析

      1.指标的选取

      本文研究区域高等教育竞争力的指标是参照“吴文”所建立的指标体系，在此指标体系的基础上，按照综合性、可比性、精简性、可操作性和可获得性的原则，有针对性地选取能反映高等教育持续发展能力的指标，由此在高等教育的资源、质量、投入、规模、效率和产出6个方面选取了每个大学教师负担学生数(人)、每万人高等院校数(所)、每万人在校大学生数(人)、人均教育经费(元)、平均每所大学在校学生数(人)、大学毕业生数(人)和6岁及以上人口中大专以上文化程度人数比(％)7个指标。以上7个指标的具体数据均来源于2005年的《中国统计年鉴》。

      2.因子分析

      把各地区以上7个指标的数据输入SPSS11.0统计软件包，在进行因子分析之前，首先要对样本数据进行取样适宜性检验，常用的检验统计量为KMO(Kaiser-Meyer-Olkin Measure of Sampling Adequacy)指标。当KMO值较小时，表明观测变量间的共同因素较少，不适合做因子分析。通常对该指标值的优劣判断标准为：该指标值在0.9以上，非常好；0.8—0.9，好；0.7—0.8，一般；0.5—0.6，差；0.5以下，不能接受[7] (P.2)。通过运算得出这7个指标的KMO值为0.693(见表1)，接近0.7，基本上属于一般水平，本文认为以上7个指标可以进行因子分析。

      表1 适宜性检验KMO测度值

      

      运用SPSS11.0统计软件包进行因子分析运算，对各个指标值的标准化变量用主成分法按特征向量λ和累计贡献率≥85％选择主成分，因此选定了2个主因子并产生各指标的因子矩阵，同时计算其特征值、贡献率和累计贡献率(见表2)。从表2中可以看出主因子1的特征值为3.908，主因子2的特征值为2.380，这2个主因子的累计贡献率达89.832％，这就可以共同解释原始变量标准化方差的89.832％，即只要选择前2个主因子，其所代表的信息量已能比较充分地解释并提供原始数据所能表达的信息。同时主因素方差(Communalities)在0.760—0.978之间，说明全体变量能很好地被这2个主因子解释。所以，选择这2个主因子的信息已能比较充分地反映和代表各地区的综合水平。对提取的2个主因子建立原始因子载荷矩阵，同时为了便于对各因子载荷作出合理解释，需要对其进行旋转，使其结构简化，排除干扰。由于所选取的反映高等教育竞争力的7个指标之间存在着正相关现象，并且有的指标之间的相关系数还很大，所以本文在用主成分方法(Principal Components)提取主因子时，进行方差极大斜交旋转(Promax with kisser Normalizaion)，从而使其结构简单化，最后得到了斜交因子装载矩阵(见表3)。进而计算得到了由原始变量指标的线形组合构成的新的综合变量。旋转以后得到的斜交因子装载矩阵将指标值按照斜交旋转因子矩阵中的高载荷分成2类。

      表2 区域高等教育竞争力因子特征值、累计比例值和累计贡献率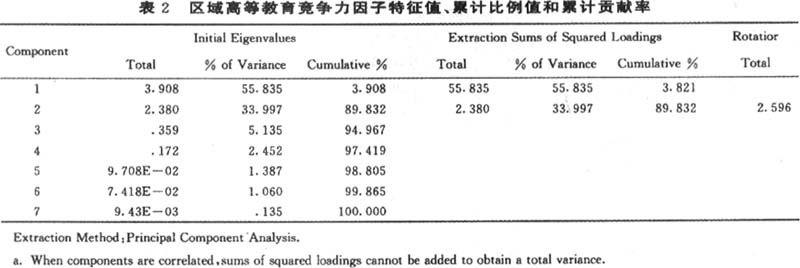

      

      Extraction Method:Principal Component Analysis.

      a.When components are correlated,sums of squared loadings cannot be added to obtain a total variance.

      表3 区域高等教育竞争力斜交主因子模型矩阵和结构矩阵