从博弈论解析大学生择业过程中的违约现象

      随着高校扩招以后，高校毕业生人数逐年递增，如今大学生普遍感到就业压力很大。虽然对于大学生来说谋得一份职业并不容易，但是大学生签约又违约的“跳槽”现象却越来越普遍。这种现象已经引起了社会的广泛关注，也产生了不少的争议。根据有关资料显示，就业过程中的违约大部分是学生所为，相对来说用人单位主动提出违约的并不多。按理说大学生在签约之前都经过了认真思考，而且要经过面试和复试才能签约，况且违约后要缴纳一大笔罚金，可是大学生违约现象却仍屡见不鲜。大学毕业生为何频频违约？本文将运用博弈论的模型、机制设计理论对大学生就业过程中的违约现象进行深层剖析，同时对解决这一问题提出一些建议。

      一、用博弈理论解析毕业生在择业过程中的违约现象

      博弈论是研究决策主体的行为发生直接相互作用时的决策以及这种决策的均衡，也就是说，当一个主体的选择受到其他主体选择的影响，而且反过来影响到其他主体选择时的决策问题和均衡问题。从博弈论的观点看，在毕业生就业市场上，用人单位和毕业生可看作是具有决策的相互独立的主体，它们都有自己的目标利益。用人单位希望通过设计一个人才吸引机制或称博弈规则来吸引毕业生，并从中挑选出最优秀、最合适的人才，他们总希望应用这种机制能使招聘的大学生有积极性来配合自己实现自身的利益和目标。而对于大学生来说，他们并没有责任和义务牺牲自己的利益去追求用人单位的最优利益，相反他们可能去追求自己的利益而把单位的利益放在次要的位置，甚至以牺牲用人单位的利益为代价，他们总是希望自己所签约的单位是最理想的选择。因此，两者的利益往往并不一致。由于毕业生和用人单位之间的信息不对称，双方需要通过多次选择或博弈才能达到某种“稳定”状态，即签订就业协议。

      毕业生和用人单位之间这种互相选择的过程可看作是一种博弈，博弈的本质是动态的你得我失，其结果未必均衡，但长期的博弈必然达到动态均衡。从短期看，就业协议的签订意味着博弈双方的利益达到了一致，即处于暂时的均衡。随着双方对彼此信息了解的增加以及其它因素的影响，这一“暂时均衡”状态就有可能失去平衡，于是违约行为开始出现，所以从长期来看，毕业生择业过程中的违约行为是一种必然现象。

      “囚徒困境”是博弈论中一个经典模型，讲的是两个嫌疑犯作案后被警方抓住，隔离审讯。警方的政策是“坦白从宽，抗拒从严”，如果两人都坦白则各判8年；如果一人坦白另一人抵赖，坦白的放出去，抵赖的判10年；如果都抵赖则因证据不足各判1年。在这个例子里，博弈的参加者就是两个嫌疑犯A和B，他们每个人都有两个策略即坦白和抵赖，判刑的年数就是他们的支付。可能出现的四种情况：A和B均坦白或均抵赖、A坦白B抵赖或者B坦白A抵赖，矩阵中的数值即是博弈的结果。

      附图

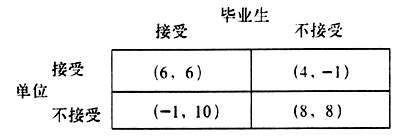
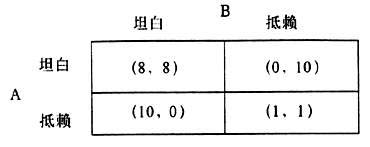      图1 嫌疑犯的支付矩阵

      A和B均坦白是这个博弈的纳什均衡。这是因为，假定A选择坦白的话，B最好是选择坦白，因为B坦白判8年而抵赖却要判10年；假定A选择抵赖的话，B最好还是选择坦白，因为B坦白不被判刑而抵赖却要被判刑1年。即是说，不管A坦白或抵赖，B的最佳选择都是坦白。反过来，同样地不管B是坦白还是抵赖、A的最佳选择也是坦白。结果，两个人都选择了坦白，各判刑8年。在（坦白，坦白）这个组合中，A和B都不能通过单方面的改变行动增加自己的收益，于是谁也没有动力游离这个组合，因此这个组合是纳什均衡。

      “囚徒困境”反映了个人理性和集体理性的矛盾。如果A和B都选择抵赖，各判刑1年，显然比都选择坦白各判刑8年好得多。当然，A和B可以在被警察抓到之前订立一个“攻守同盟”，但是这可能不会有用，因为它不构成纳什均衡，没有人有积极性遵守这个协定。

      “囚徒困境”模型在经济学中有广泛应用，也可以用来解释现实中的很多问题，我们不妨用它来分析毕业生择业过程中的违约行为。如果用人单位和毕业生都有违约意向，即双方对违约都持赞成态度，用人单位可以继续招收员工，毕业生也可以顺利地进入第二次就业程序，双方损失仅为签约和招聘成本，可忽略不计，可将两者的支付水平设为（6，6）；假设毕业生和用人单位均无违约意向，毕业生将顺利进入单位工作，双方对自己的利益都很满意，可认为达到最佳组合，不妨将支付水平设为（8，8）；假设毕业生单方面违约，而用人单位不愿接受，往往是由于毕业生找到更满意的工作而拒绝到原签约单位工作，这对用人单位损失较大，得不到任何的好处，而毕业生由于有强烈的流动意向，虽说损失了暂时利益（如支付违约金等），但从长远来说，会拥有了称心如意的工作，必将得到比不违约时还要高的支付水平，二者支付水平可设为（－1，10）；假设用人单位签约后发现毕业生并不适合当前工作，有违约意向，而毕业生不肯接受，则用人单位就会采取某些措施使学生解除协议（比如支付违约金等），这样就可以为自己引进合适的人才，其支付肯定比留下来继续使用要高，但总会比双方同意解除协议要低，而毕业生由于还未正式上班便被“炒”，其损失较大，两者支付水平可设为（4，－1）。

      附图