高校合并的经济学分析

      中图分类号：F08;G40-054　文献标识码：A　文章编号：1003-4870(2003)02-0049-04

      前两年，随着我国高等教育管理体制改革的不断深化，国家和省级教育主管部门为适应经济体制改革和社会发展的需要，积极推进高教管理体制改革，扩大高等教育规模，调整高等教育结构，掀起了一轮“高校合并潮”。应当说，这是我国新世纪高等教育改革和发展的一项重大战略举措。但是，高校合并办学能否取得预期的成效，能否真正实现实质性的深度融合，取决于多方面的因素。为此，本文应用经济学的一般原理，对高校合并办学的若干问题进行理性分析。

      一、教育成本及成本函数

      教育总成本(TC)是指特定范围内使用的一切教育资源成本。对于某一所大学来说，教育总成本是指一所大学的办学成本总额。教育总成本等于固定成本与变动成本之和。固定成本是指在一定时间和一定学生数量范围内，成本发生总额不受学生数量增减的影响而相对固定的成本。包括教育占用固定资产（如教室、宿舍、教学仪器设备、体育设施、图书资料等）及其折旧费、水电费、维修费，教职工的基本工资、办公费、差旅费等。在某一学生数量范围内，固定成本是不变的，当学生数量发生很大的变化（急剧增加或减少）时，教育的固定成本会相应增加或减少，如新建教学基础设施、添置设备、提高工资等。教育变动成本是指教育成本发生额中随学生数量增减而变动的那部分费用，包括教职工的奖金、超工作量报酬、兼职或代课教师工资、学生的奖助学金，用于教学和生产实习的材料费、低值易耗费、实习实验费等。

      在一定时期内，学校的教育总成本与学生数量的比值称为教育平均成本(AC)。它包括教育平均固定成本和教育平均变动成本两部分。由每增加一名学生导致的成本增量称为教育边际成本(MC)。

      教育成本与学生数量有函数关系，[1]如1、图2所示（图见下页）。

      用TC代表总成本，AC代表平均成本，MC代表边际成本，n代表在校学生数量，那么TC、AC、MC与学生数量之间的关系可由下式表示：

      TC=f(n)=a[,0]+a[,1]n

      AC=TC/n=a[,0]/n+a[,1]

      MC≈Δ(TC)/Δn=d(TC)/dn=a[,1]

      上式中，a[,0]是固定成本，a[,1]是每增加一名学生所导致的成本增加额，即边际成本。

      在现实生活中，学生增长的量不同，其成本的增量也不同，所以其函数表达式更为复杂。

      假设：TC=a[,0]+a[,1]n+a[,2]n[2]+a[,3]n[3]

      推出：AC=TC/n=a[,0]/n+a[,1]+a[,2]n+a[,3]n[2]

       MC=d(TC)/dn=a[,1]+2a[,2]n+3a[,3]n[2]

      用曲线图表示如图3。

      

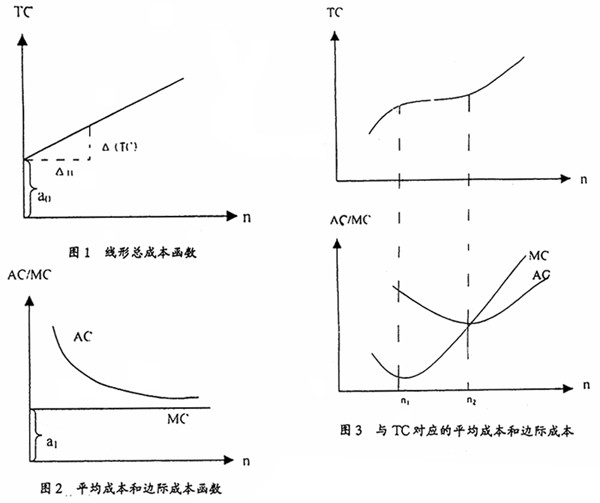      二、合并办学的规模效益分析

      学校规模问题是教育经济学中研究的重要内容。20世纪80年代，学校规模优化还是一种设想，随着90年代高校合并的出现，不断扩大高校规模已经成为现实，如何实现高校规模效益，也就成为人们关注的重要问题。鲁姆勃尔在其教育的财务和成本分析模式结构中，用生均成本——学生数关系曲线来反映教育规模扩大，可带来生均成本的降低这样一种规律。[2]90年代初闵维方等人采用回归方法，对我国高等学校生均成本与学校规模之间的关系作了分析，结论是“高等教育生均成本随着学校规模的扩大和生师比的提高而下降”。[3]这些研究成果表明，通过高校合并，不仅可以提高大学的毛入学率，满足社会对高等教育的需求，而且为降低生均成本，提高规模效益提供了可能。

      高校合并的目的之一是扩大办学规模，降低办学成本，提高办学效益。如果高校合并并不能带来规模效益的递增，那么这种合并就缺乏经济上的可行性。

      从图2中分析可以看出，随着学生数量的增长，AC稳步下降，表示有规模效益。这是假设在办学固定成本不变的情况下，随着学生数量(n)的增长，固定成本a[,0]在较大学生数量上的均摊而减小。但在学生数量(n)很大的情况下，AC与MC非常接近，即平均成本接近于边际成本，规模效益最终枯竭。

      由图3可见，在学生人数增加到n[,2]时，平均成本随学生数量增长而降低，这与图2的变化规律相似。其原因有两个方面：一是学生数量越大，固定成本a[,0]在学生中的均摊越小；二是学生数增加到n[,1]时，边际成本MC下降，对平均成本AC的降低起了一定的积极作用。但学生数在n[,1]与n[,2]之间，边际成本呈现上升趋势，最终在学生数增加到n[,2]时，抵消了平均成本的降低。超过n[,2]，边际成本增加的影响占支配地位，每增加一名学生而导致的办学成本增量变大，规模效益消失，平均成本也开始上升。通过对MC和AC之间的关系分析可知：

      1.MC=AC，学校规模效益中性，不管学生数量多少，平均成本保持不变。