中图分类号：G640 文献标识码：A 文章编号：1008-7494(2000)04-0001-04 高等教育决策是高等教育管理工作的重要组成部分。所谓决策，就是从许多为达到同一高等教育目标而可交换替代的行动方案中评价选择一个最优方案的过程。表面上看决策是一些简单的日常工作，但稍作分析，就会发现事情并非那么简单，原因在于其中或多或少地夹杂着某些不确定性。这种不确定性，既有随机不确定，例如新学年到底能招多少新生就是一个带有随机性的问题；也有模糊不确定，例如建造一座实验楼，不同的建造方案有不同的造价，同一个方案让不同的建筑公司来投标，标的也会有差异，说明其中存在模糊性。可见，决策的要害就在于如何科学合理地认识、分析和把握其中的不确定性。由我国学者赵克勤先生提出的集对分析和联系数，为处理决策中的不确定性提供了一种新的数学工具[1][2]。本文尝试着把集对分析和联系数引入到高教决策中，并结合一些实例作具体说明。 一、集对分析和联系数简介 （一）集对分析 所谓集对，是指具有一定联系的两个集合所作成的对子。集对分析(Set Pair Analysis简记为SPA）的基本思路是通过分析所论两个集合的特性，建立起所论两个集合在指定问题背景下的联系度表达式u=a+bi+cj，再推广到研究对象由多个集合组成时的情况，在此基础上开展有关问题的研究。其中a、b、c分别称为同一度、差异度、对立度，a+b+c=1,j=-1,i在[-1,1]区间视不同情况不确定取值。例如某班级50名学生，某门课成绩优秀的为15人，中等的为30人，成绩差的为5人，则可以用u=15/50+30/50i+5/50j=0.3+0.6i+0.1j来表示该班学生这门课的总体学习成绩状况。这里的j是成绩“差”的标记，i则在[-1,1]之间不确定取值，以表示处于中间状态的这部分有较大的不确定性，i取正值，表示这部分学生的成绩向“优秀”进步；i取负值，表示这部分学生的成绩向“差”滑动，i的绝对值大小反映了中间这部分学生向“优秀”与“差”两极分化的比例。 （二）联系数 由文献[1][2]可知，联系数a+bi脱胎于集对分析中的同异反联系度a+bi+cj。在联系度意义下，有a+b+c=1这一约束条件。而在联系数意义下，a+bi中的a、b可以是任意非负实数，但i仍在[-1,1]区间不确定取值。这样，尽管在一个具体的联系数a+bi中我们让a、b以具体的定值出现，但由于i的作用，a+bi的既确定又不确定性为不少问题的研究带来了方便。例如某学生对自己考数学得80分认为是有把握的，考80分以上到100分，认为不确定，则可记为80+20i。当i在[-1,1]不确定取值时，该考生的实际成绩将在60-100分之间。这个例子表明，在一个既确定又不确定的系统中，不确定性与确定性是互相联系、互相制约、互相影响且可以在一定条件下互相转化的。 据有关文献资料，集对分析和联系数在教育、管理、决策等方面已得到应用[3][4][5]。 二、基于集对分析和联系数的高等教育决策方法及应用 借助集对分析和联系数，我们可以方便且成功地解决一些高等教育决策问题。笔者将这两种高等教育决策新方法分别称之为同一度法、联系数法。 （一）第一种决策方法：同一度法 [例1]某高校欲建闭路电视网，已知有A[,1]、A[,2]、A[,3]三种建设方案，每个方案的指标、指标权重及指标值见表1，试问宜采用哪个方案。
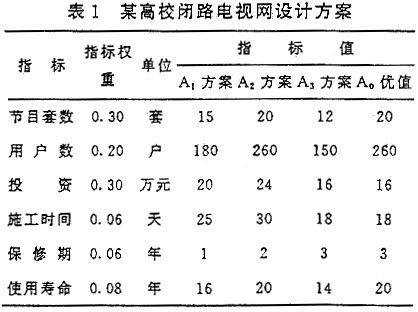
这一类决策实际上是要在多个可行方案中择优选用其一的问题。应用集对分析同一度概念求解以上问题的方法与步骤如下： 第一步：根据给出的A[,1]，A[,2]，…A[,n]共n个方案，确定出一个理想方案A[,0]。 规定A[,0]中各指标的取值应是被评价的n个方案中各类指标的最优值，即对于效益型指标来说取其最大值，对于成本型指标来说取其最小值，并记A[,0]中第K个指标的值为f[,0]pk。相应地记被评价方案A[,i]中第K个指标的值为fipk。据表1给出的各指标情况，易知理想方案中各指标取值情况应是节目为20套、用户为260户、投资为16万元、施工为18天、保修期为3年、使用寿命为20年。为便于对照，这些数值已列在表1的最右一列。 第二步：计算被评价方案中各指标值fipk与理想方案A[,0]中各对应指标值f[,0]pk的同一度，a[,ik]组成被评价方案指标与理想方案指标的联系矩阵H。
第四步：根据R中的n个a[,i]值的大小次序确定出n个被评价方案的优劣次序。a[,i]值大的方案较a[,i]值小的方案为优。由于0.856＞0.771＞0.731，所以在给出的A[,1]，A[,2]，A[,3]三个方案中以方案A[,2]最优，方案A[,3]次之，方案A[,1]最差。因此，例1决策结果为宜采用方案A[,2]建设闭路电视网。 以上对同一度法作了介绍，这种方法可以推广到多个可行方案的评价与择优。需要说明的是：第一，例1中为叙述方便起见，事先假定方案中的指标权重为已知。实际工作时，可采用专家评分办法确定出组成方案各指标的权重，再采用本文所述之方法开展工作；第二，集对分析的思想方法是对所研究的对象作同异反定量刻划和分析，但若问题本身不需要对所论集对作差异性和对立性分析的话，则只要对研究对象作同一性分析和作同一度的刻划计算就可以了。故这种决策方法称之为同一度法。
